深度学习-Course2-Week2优化算法
1 Mini-batch梯度下降
之前我们介绍的神经网络训练过程是对所有m个样本,称为batch,通过向量化计算方式,同时进行的。
如果m很大,例如达到百万数量级,训练速度往往会很慢,因为每次迭代都要对所有样本进行求和运算和矩阵运算。我们将这种梯度下降算法称为Batch Gradient Descent。
为了解决这一问题,我们可以把m个训练样本分成若干个子集,称为mini-batches,这样每个子集包含的数据量就小了,例如只有1000,然后每次在单一子集上进行神经网络训练,速度就会大大提高。这种梯度下降算法叫做Mini-batch Gradient Descent。
假设总的训练样本个数m=5000000,其维度为$(n_x,m)$。将其分成5000个子集,每个mini-batch含有1000个样本。我们将每个mini-batch记为$X^$,其维度为$(n_x,1000)$。相应的每个mini-batch的输出记为$Y^$,其 维 度 为 (1,1000),且$t=1,2,\cdots,5000$。
这里顺便总结一下我们遇到的神经网络中几类字母的上标含义:
$X^{(i)}:$ 第i个样本
$Z^{[l]}:$ 神经网络第$l$层网络的线性输出
$X^,Y^:$ 第t组mini-batch
Mini-batches Gradient Descent的实现过程是先将总的训练样本分成T个子集(mini-batches),然后对每个mini-batch进行神经网络训练,包括向前传播,计算Cost Function,反向传播,循环至T个mini-batch都训练完毕。
1 | |
经过T次循环之后,所有m个训练样本都进行了梯度下降计算。这个过程,我们称之为经历了一个epoch。
对于Batch Gradient Descent而言,一个epoch只进行一次梯度下降算法;而Mini-Batches Gradient Descent,一个epoch会进行T次梯度下降算法。
值得一提的是,对于Mini-Batches Gradient Descent,可以进行多次epoch训练。而且,每次epoch,最好是将总体训练数据重新打乱、重新分成T组mini-batches,这样有利于训练出最佳的神经网络模型。
Batch gradient descent和Mini-batch gradient descent的cost曲线如下图所示:
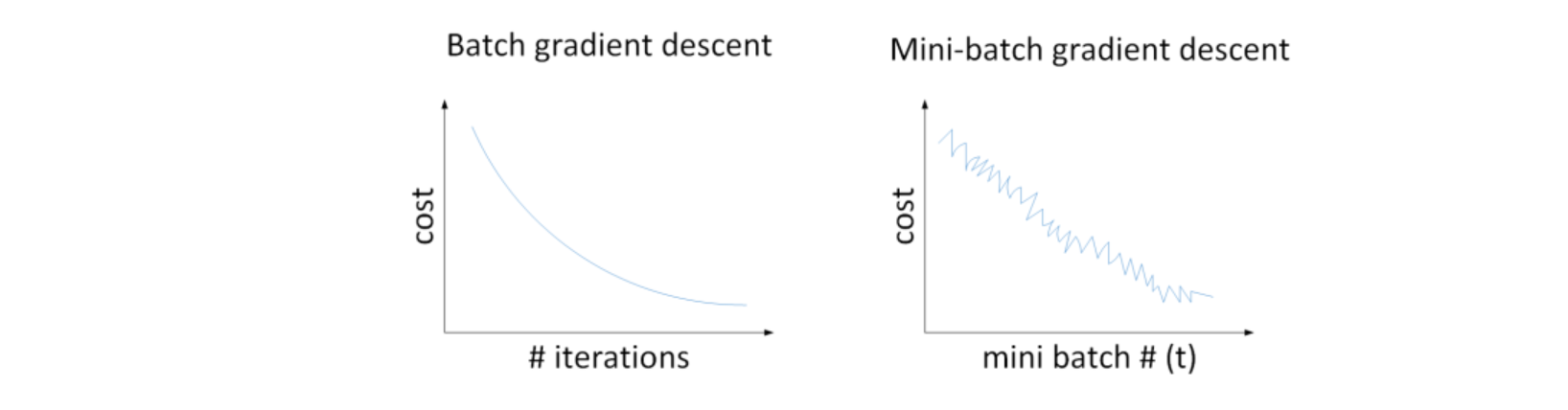
对于一般的神经网络模型,使用Batch gradient descent,随着迭代次数增加,cost是不断减小的。然而,使用Mini-batch gradient descent,随着在不同的mini-batch上迭代训练,其cost不是单调下降,而是受类似noise的影响,出现振荡。但整体的趋势是下降的,最终也能得到较低的cost值。
之所以出现细微振荡的原因是不同的mini-batch之间是有差异的。例如可能第一个子集$(X^1,Y^1)$是好的子集,而第二个子集$(X^2,Y^2)$包含了一些噪声noise。出现细微振荡是正常的。
如何选择每个mini-batch的大小,即包含的样本个数呢?有两个极端:如果mini-batch size=m ,即为Batch gradient descent ,只包含一个子集 为$(X^1,Y^1)=(X,Y)$ ;如果mini-batch size=1 , 即为Stachastic gradient descent,每个样本就是一个子集$(X^1,Y^1)=(x^{(i)},y^{(i)})$ ,共有m个子集。
我们来比较一下Batch gradient descent和Stachastic gradient descent的梯度下降曲线。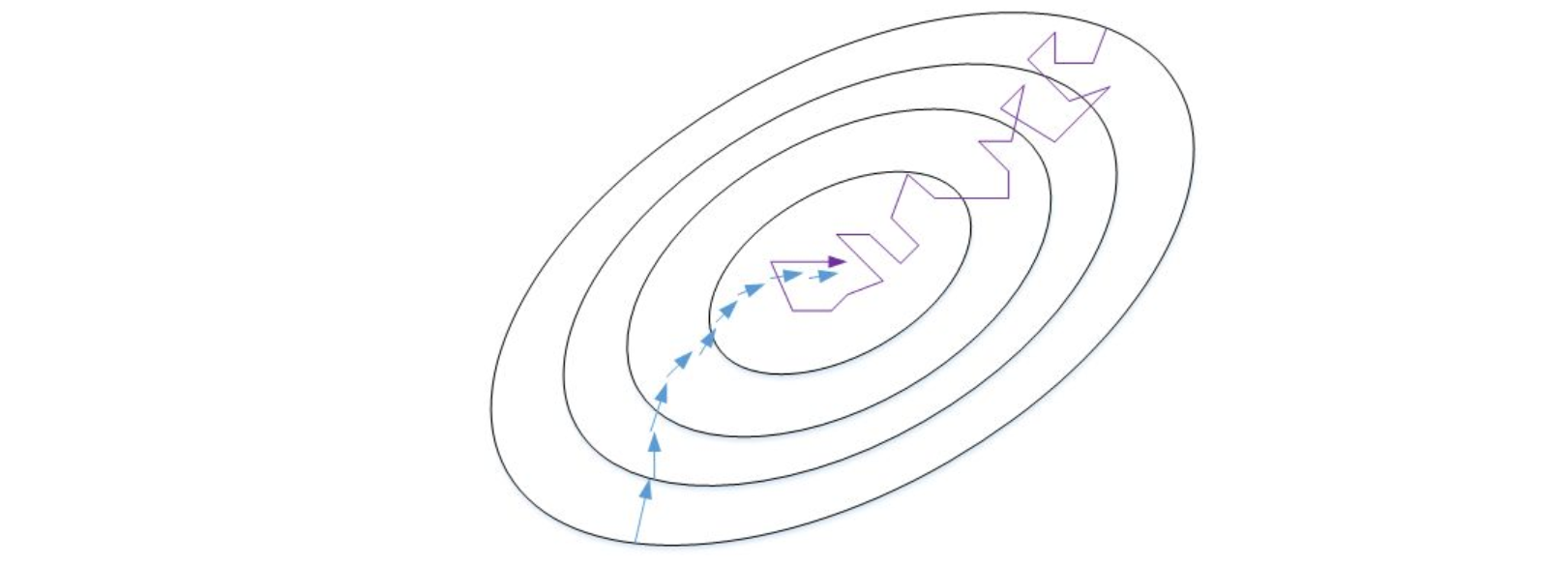
如图所示,蓝色的线代表Batch gradient descent,紫色的线代表Stachastic gradient descent。
Batch gradient descent会比较平稳地接近全局最小值,但是因为使用了所有m个样本,每次前进的速度有些慢。
Stachastic gradient descent每次前进速度很快,但是路线曲折,有较大的振荡,最终会在最小值附近来回波动,难以真正达到最小值处。而且在数值处理上就不能使用向量化的方法来提高运算速度。
实际使用中,mini-batch size不能设置得太大(Batch gradient descent),也不能设置得太小(Stachastic gradient descent)。
这样,相当于结合了Batch gradient descent和Stachastic gradient descent各自的优点,既能使用向量化优化算法,又能较快速地找到最小值。
mini-batch gradient descent的梯度下降曲线如下图绿色所示,每次前进速度较快,且振荡较小,基本能接近全局最小值。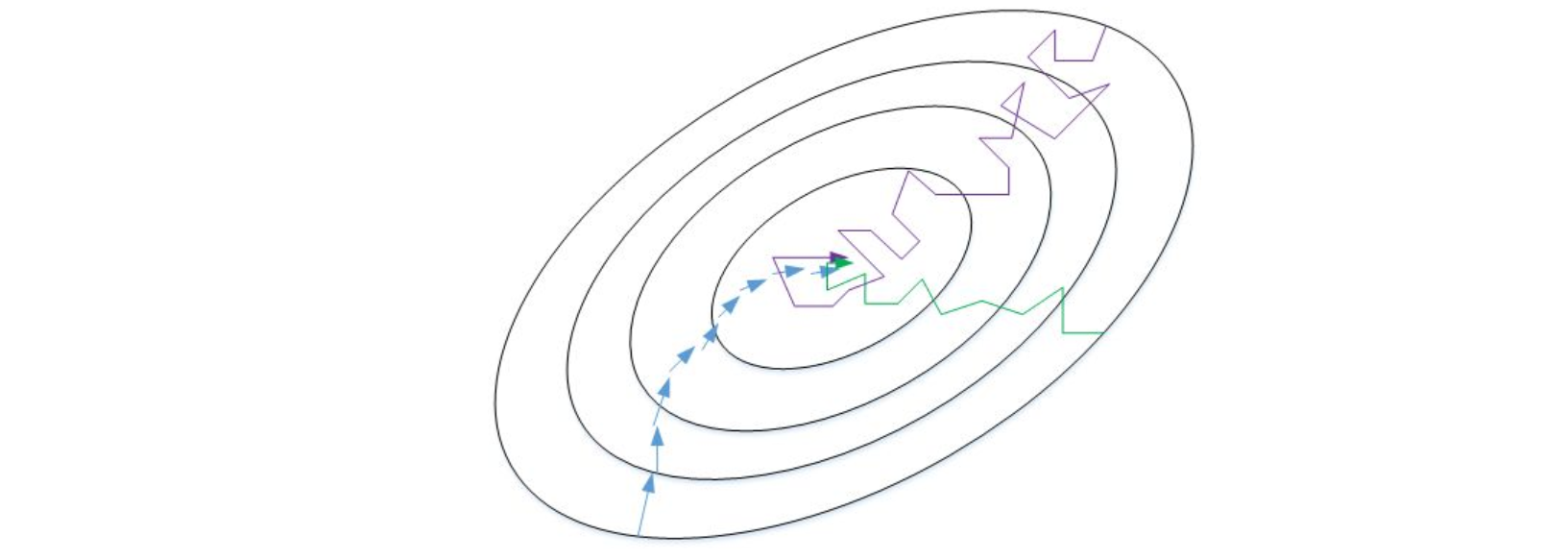
一般来说,如果总体样本数量m不太大时,例如m≤2000m≤2000,建议直接使用Batch gradient descent。
如果总体样本数量m很大时,建议将样本分成许多mini-batches。推荐常用的mini-batch size为64,128,256,512。这些都是2的幂。
之所以这样设置的原因是计算机存储数据一般是2的幂,这样设置可以提高运算速度。
2 指数加权平均
指数加权平均概念
该部分我们将介绍指数加权平均(Exponentially weighted averages)的概念。
我们记录半年内伦敦市的气温变化,并在二维平面上绘制出来,如下图所示:
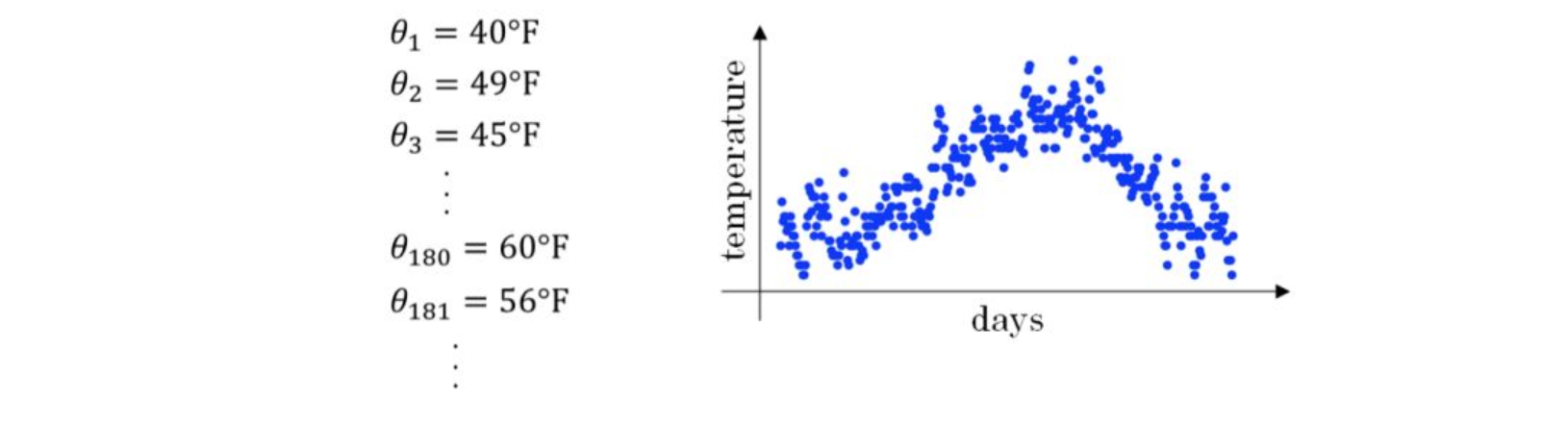
如果我们希望看到半年内气温的整体变化趋势,可以通过移动平均(moving average)的方法来对每天气温进行平滑处
例如我们可以设V0=0,当成第0天的气温值。
第一天的气温与第0天的气温有关:
$$V_1=0.9V_0+0.1\theta_1$$
第二天的气温与第一天的气温有关:
$$V_2=0.9V_1+0.1\theta_2$$
第三天的气温与第二天的气温有关:
$$V_3=0.9V_2+0.1\theta_3$$
即第t天与第t-1天的气温迭代关系为:
$$V_t=0.9V_{t-1}+0.1\theta_t$$
经过移动平均处理得到的气温如下图红色曲线所示: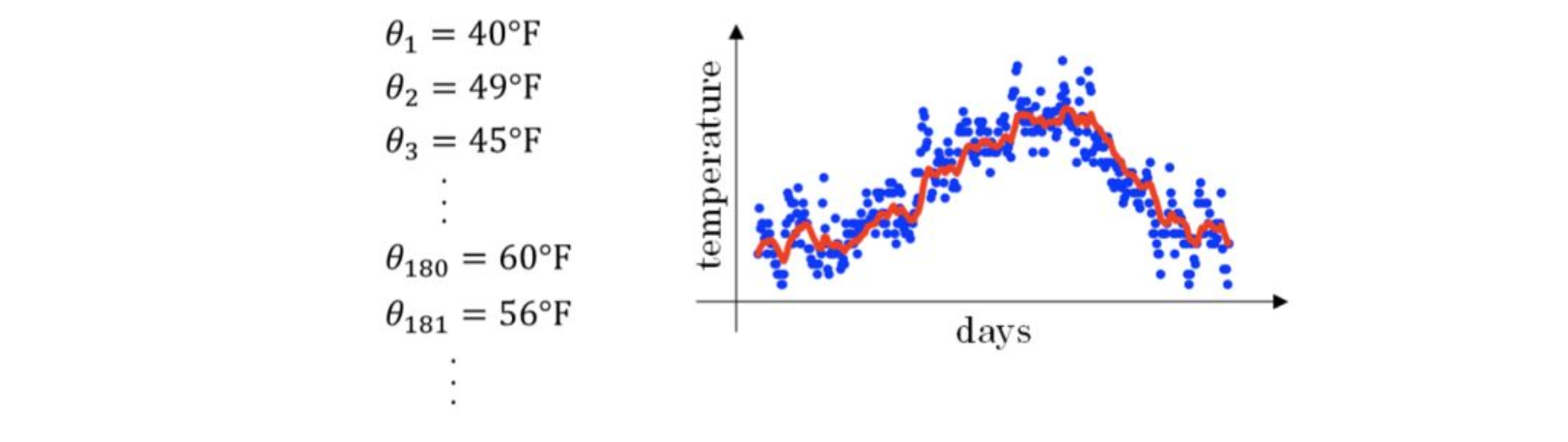
这种滑动平均算法称为指数加权平均(exponentially weighted average)。根据之前的推导公式,其一般形式为:
$$V_t=\beta V_{t-1}+(1-\beta)\theta_t$$
上面的例子中,β=0.9。β值决定了指数加权平均的天数,近似表示为$\frac1{1-\beta}$
例如,当$\beta=0.9$,则$\frac{1}{1-\beta}=10$,表示将前10天进行指数加权平均。当$\beta=0.98$,则$\frac{1}{1-\beta}=50$,表示将前50天进行指数加权平均。$\beta$值越大,则指数加权平均的天数越多,平均后的趋势线就越平缓,但是同时也会向右平移。下图绿色曲线和黄色曲线分别表示了$\beta=0.98$和$\beta=0.5$时,指数加权平均的结果。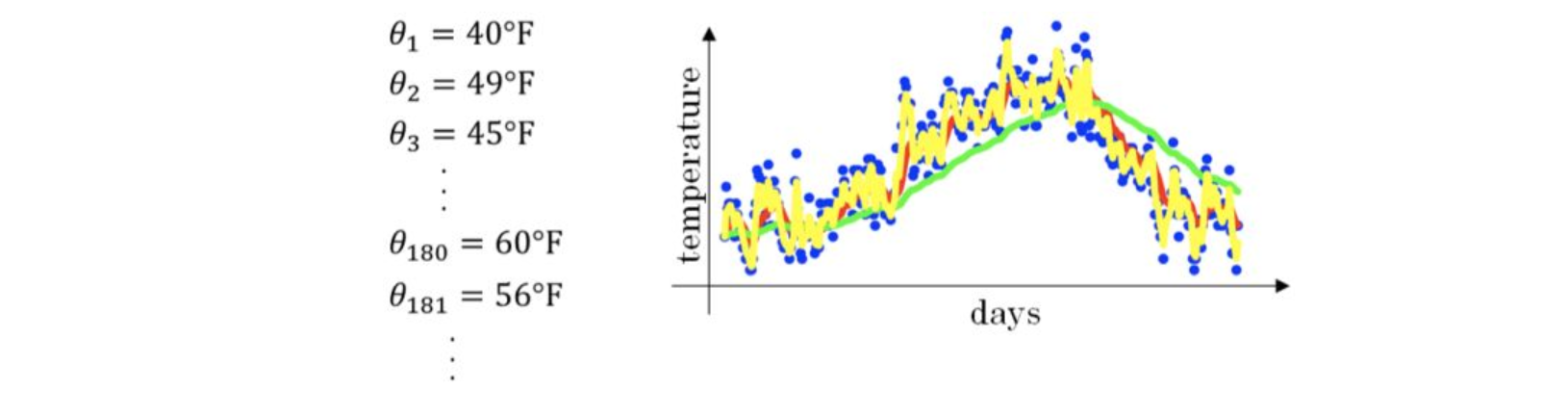
这里简单解释一下公式1/(1−β)是怎么来的。准确来说,指数加权平均算法跟之前所有天的数值都有关系,根据之前的推导公式就能看出。
但是指数是衰减的,一般认为衰减到1/e就可以忽略不计了。因此,根据之前的推导公式,我们只要证明下式就好了:
$$
\beta^{\frac1{1-\beta}}=\frac1e
$$
令$\frac{1}{1-\beta}=N$ ,$N>0$ ,则$\beta=1-\frac{1}{N}$ ,$\frac{1}{N}<1$。即证明转化为:
$$(1-\frac1N)^N=\frac1e$$
显然,当N>>0时,上述等式是近似成立的。
至此,简单解释了为什么指数加权平均的天数的计算公式为1/(1−β)。
偏差修正
上文中提到当β=0.98时,指数加权平均结果如下图绿色曲线所示。但是实际上,真实曲线如紫色曲线所示。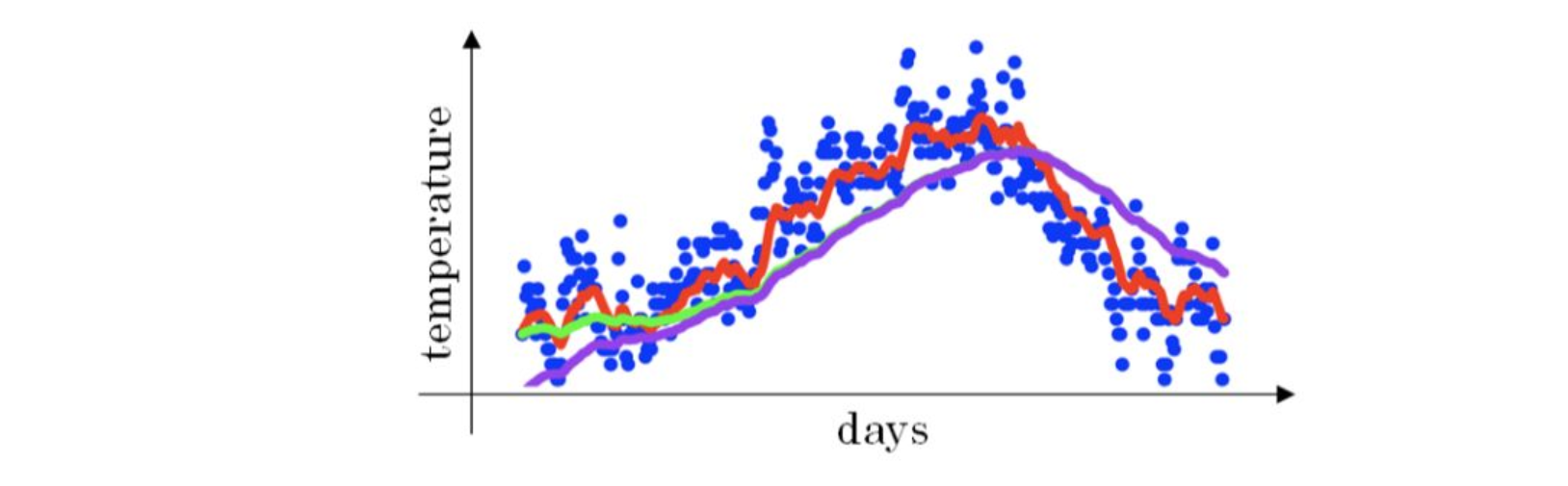
我们注意到,紫色曲线与绿色曲线的区别是,紫色曲线开始的时候相对较低一些。这是因为开始时我们设置V0=0,所以初始值会相对小一些,直到后面受前面的影响渐渐变小,趋于正常。
修正这种问题的方法是进行偏移校正(bias correction),即在每次计算完Vt后,对Vt进行下式处理:$\frac{V_t}{1-\beta^t}$
在刚开始的时候,t比较小,$(1-\beta^t)<1$,这样就将$V_t$修正得更大一些,效果是把紫色曲线开始部分向上提升一些,与绿色曲线接近重合。随着t增大$(1-\beta^t)\approx1$,$V_t$基本不变,紫色曲线与绿色曲线依然重合。这样就实现了简单的偏移校正,得到我们希望的绿色曲线。
值得一提的是,机器学习中,偏移校正并不是必须的。因为,在迭代一次次后(t较大),Vt受初始值影响微乎其微,紫色曲线与绿色曲线基本重合。所以,一般可以忽略初始迭代过程,等到一定迭代之后再取值,这样就不需要进行偏移校正了。
3 动量梯度下降算法
该部分将介绍动量梯度下降算法,其速度要比传统的梯度下降算法快很多。做法是在每次训练时,对梯度进行指数加权平均处理,然后用得到的梯度值更新权重W和常数项b。下面介绍具体的实现过程。
原始的梯度下降算法如上图蓝色折线所示。在梯度下降过程中,梯度下降的振荡较大,尤其对于W、b之间数值范围差别较大的情况。此时每一点处的梯度只与当前方向有关,产生类似折线的效果,前进缓慢。
而如果对梯度进行指数加权平均,这样使当前梯度不仅与当前方向有关,还与之前的方向有关,这样处理让梯度前进方向更加平滑,减少振荡,能够更快地到达最小值处。
这是因为之前的梯度方向可以保证是大致指向极小值方向的,而当前的可能是也可能不是,因此如果是,则用之前的梯度加强其收敛速度,否则用之前的去抵消以减弱收敛速度,这种方法的问题即容易积累动量从而越过极小值。
权重W和常数项b的指数加权平均表达式如下:
$$\begin{aligned}V_{dW}&=\beta\cdot V_{dW}+(1-\beta)\cdot dW\V_{db}&=\beta\cdot V_{db}+(1-\beta)\cdot db\end{aligned}$$
初始时,令Vdw=0,Vdb=0。一般设置β=0.9,即指数加权平均前10天的数据,实际应用效果较好。
另外,关于偏移校正,可以不使用。因为经过10次迭代后,随着滑动平均的过程,偏移情况会逐渐消失。
4 RMSprop
RMSprop是另外一种优化梯度下降速度的算法。每次迭代训练过程中,其权重W和常数项b的更新表达式为:
$$\begin{gathered}
S_W=\beta S_{dW}+(1-\beta)dW^2 \
S_b=\beta S_{db}+(1-\beta)db^2 \
W:=W-\alpha\frac{dW}{\sqrt{S_{W}}},b:=b-\alpha\frac{db}{\sqrt{S_{b}}}
\end{gathered}$$
下面简单解释一下RMSprop算法的原理,仍然以下图为例,为了便于分析,令水平方向为W的方向,垂直方向为b的方向。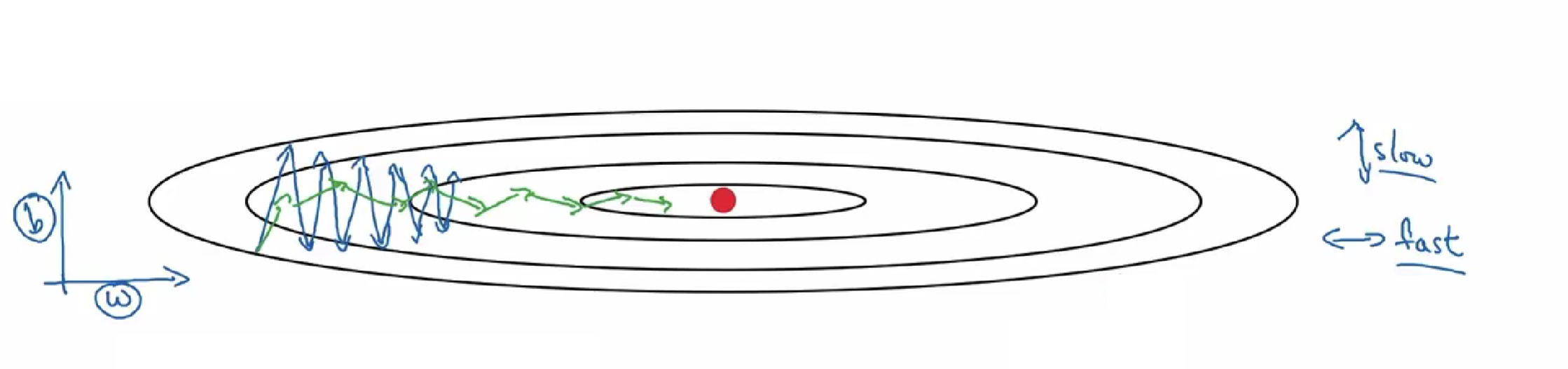
从图中可以看出,梯度下降(蓝色折线)在垂直方向 (b)上振荡较大,在水平方向(W)上振荡较小,表示在b方向上梯度较大,即$db$较大,而在W方向上梯度较小,即$dW$较小。因此,上述表达式中$S_{b}$较大,而$S_W$较小。在更新W和b的表达式中,变化值 $\frac{dW}{\sqrt{Sw}}$较大,而$\frac{db}{\sqrt{S_b}}$较小。也就使得W变化得多一些,b变化得少一些。即加快了W方向的速度,减小了b方向的速度,减小振荡,实现快速梯度下降算法,其梯度下降过程如绿色折线所示。总得来说,就是如果哪个方向振荡大,就减小该方向的更新速度, 从而减小振荡。
还有一点需要注意的是为了避免RMSprop算法中分母为零,通常可以在分母增加一个极小的常数ε:
$$W:=W-\alpha\frac{dW}{\sqrt{S_W}+\varepsilon},\mathrm{~}b:=b-\alpha\frac{db}{\sqrt{S_b}+\varepsilon}$$
其中,ε=10^−8,或者其它较小值。
5 Adam优化算法
Adam(Adaptive Moment Estimation)算法结合了动量梯度下降算法和RMSprop算法。其算法流程为:
$$\begin{aligned}
&V_{dW}=0,S_{dW},V_{db}=0,S_{db}=0 \
&\text{On iteration t:} \
&&&\textit{Cimpute d}W,db \
&&&\begin{aligned}V_{dW}=\beta_1V_{dW}+(1-\beta_1)dW,V_{db}=\beta_1V_{db}+(1-\beta_1)db\end{aligned} \
&&&\begin{aligned}S_{dW}=\beta_2S_{dW}+(1-\beta_2)dW^2,S_{db}=\beta_2S_{db}+(1-\beta_2)db^2\end{aligned} \
&&&V_{dW}^{corrected}=\frac{V_{dW}}{1-\beta_1^t},V_{db}^{corrected}=\frac{V_{db}}{1-\beta_1^t} \
&&&S_{dW}^{corrected}=\frac{S_{dW}}{1-\beta_2^t},S_{db}^{corrected}=\frac{S_{db}}{1-\beta_2^t} \
&&&W:=W-\alpha\frac{V_{dW}^{corrected}}{\sqrt{S_{dW}^{corrected}}+\varepsilon},b:=b-\alpha\frac{V_{db}^{corrected}}{\sqrt{S_{db}^{corrected}}+\varepsilon}
\end{aligned}$$
Adam 算法包含了几个超参数,分别是:$\alpha,\beta_1,\beta_2,\varepsilon$。其中,$\beta_1$通常设置为0.9,$\beta_2$通常设置为0.999,$\varepsilon$通常设置为$10^{-8}$。一般只需要对$\beta_{1}$和$\beta_{2}$进行调试。
实际应用中,Adam算法结合了动量梯度下降和RMSprop各自的优点,使得神经网络训练速度大大提高。
6 学习率衰减
减小学习因子α也能有效提高神经网络训练速度,这种方法被称为learning rate decay。
学习率衰减就是随着迭代次数增加,学习因子α逐渐减小。
下面用图示的方式来解释这样做的好处。下图中,蓝色折线表示使用恒定的学习因子α,由于每次训练α相同,步进长度不变,在接近最优值处的振荡也大,在最优值附近较大范围内振荡,与最优值距离就比较远。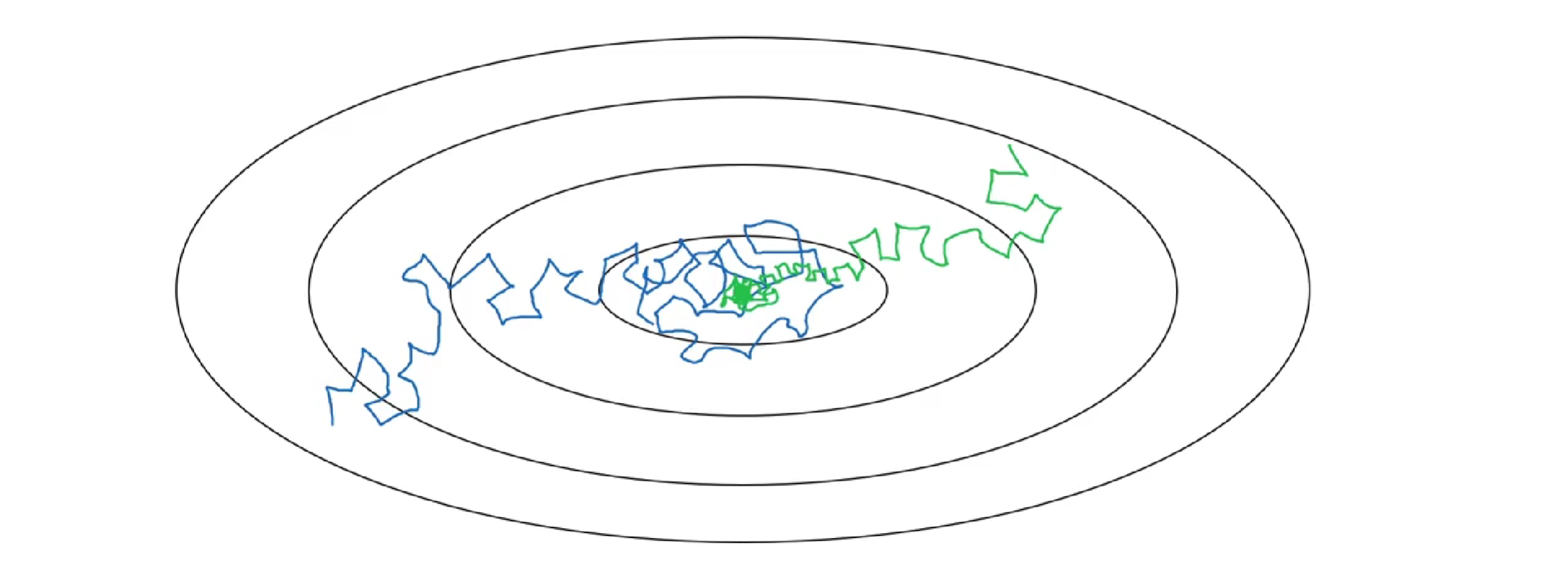
绿色折线表示使用不断减小的α,随着训练次数增加,α逐渐减小,步进长度减小,使得能够在最优值处较小范围内微弱振荡,不断逼近最优值。相比较恒定的α来说,learning rate decay更接近最优值。
Learning rate decay中对α可由下列公式得到:
$$\alpha=\frac1{1+\textit{deca}y_rate*epoch}\alpha_0$$
其中,deacy_rate是参数(可调),epoch是训练完所有样本的次数。随着epoch增加,α会不断变小。
除了上面计算α的公式之外,还有其它可供选择的计算公式:
$$\begin{gathered}\alpha=0.95^{epoch}\cdot\alpha_0\\alpha=\frac k{\sqrt{epoch}}\cdot\alpha_0\quad or\quad\frac k{\sqrt{t}}\cdot\alpha_0\end{gathered}$$
其中,k为可调参数,t为mini-bach number。
除此之外,还可以设置α为关于t的离散值,随着t增加,α呈阶梯式减小。
也可以根据训练情况手动调整当前的α值,但会比较耗时间。
7 局部最优问题
在使用梯度下降算法不断减小cost function时,可能会得到局部最优解(local optima)而不是全局最优解(global optima)。
之前我们对局部最优解的理解是形如碗状的凹槽,如下图左边所示。但是在神经网络中,局部最优解的概念发生了变化。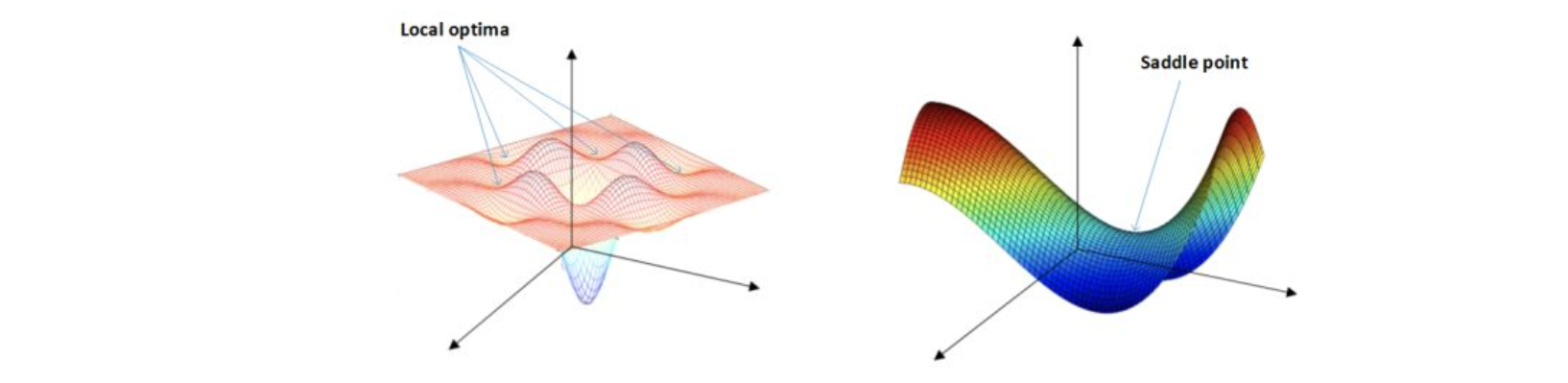
准确地来说,大部分梯度为零的“最优点”并不是这些凹槽处,而是形如右边所示的马鞍状,称为saddle point。
也就是说,梯度为零并不能保证都是convex(极小值),也有可能是concave(极大值)。
特别是在神经网络中参数很多的情况下,所有参数梯度为零的点很可能都是右边所示的马鞍状的saddle point,而不是左边那样的local optimum。
类似马鞍状的plateaus会降低神经网络学习速度。Plateaus是梯度接近于零的平缓区域,如下图所示。在plateaus上梯度很小,前进缓慢,到达saddle point需要很长时间。
到达saddle point后,由于随机扰动,梯度一般能够沿着图中绿色箭头,离开saddle point,继续前进,只是在plateaus上花费了太多时间。
总的来说,关于local optima,有两点总结:
只要选择合理的强大的神经网络,一般不太可能陷入local optima
Plateaus可能会使梯度下降变慢,降低学习速度
值得一提的是,上文介绍的动量梯度下降,RMSprop,Adam算法都能有效解决plateaus下降过慢的问题,大大提高神经网络的学习速度。