深度学习-Course2-Week1深度学习实用层面
1.1 训练,验证,测试集(Train / Dev / Test sets)
数据集划分
一般我们将所有的样本数据分成三个部分:Train/Dev/Test sets。
- 训练集(Train sets):用于训练深度学习模型。
- 验证集(Dev sets):用于验证不同算法的表现,并选择最佳的算法模型。
- 测试集(Test sets):用于测试最佳算法的实际表现,提供无偏估计。
数据集比例设定
通常设置Train sets和Test sets的数量比例为70%和30%。如果有Dev sets,则设置比例为60%、20%、20%,分别对应Train/Dev/Test sets。
对于大数据样本,可将 Dev sets 和 Test sets 的比例设置得更低,如 1% 或 0.5%。例如,对于 100 万样本,可以采用 98%/1%/1% 或 99%/0.5%/0.5% 的比例分配。
超参数优化
- 构建神经网络时需设置多个超参数,如层数、每个隐藏层神经元个数、学习速率、激活函数等。
- 通过反复迭代更新来获得最佳参数值。循环迭代过程包括:提出想法(Idea)、选择初始参数值、构建神经网络模型结构、通过代码实现神经网络、验证参数对应的神经网络性能。
- 通过多次循环调整参数并选择最佳参数值来优化神经网络性能。
训练效率提升
- 应用深度学习是一个反复迭代的过程,需要通过多次循环训练得到最优化参数。
- 循环训练的关键是单次循环所需时间,单次循环越快,训练过程越快。合适的 Train/Dev/Test sets 数量能有效提高训练效率。
1.2 偏差,方差(Bias /Variance)
偏差和方差的概念
在传统的机器学习算法中,偏差(Bias)和方差(Variance)是对立的,分别对应着欠拟合和过拟合,我们常常需要在Bias和Variance之间进行权衡。
而在深度学习中,我们可以同时减小Bias和Variance,构建最佳神经网络模型。
偏差和方差的权衡
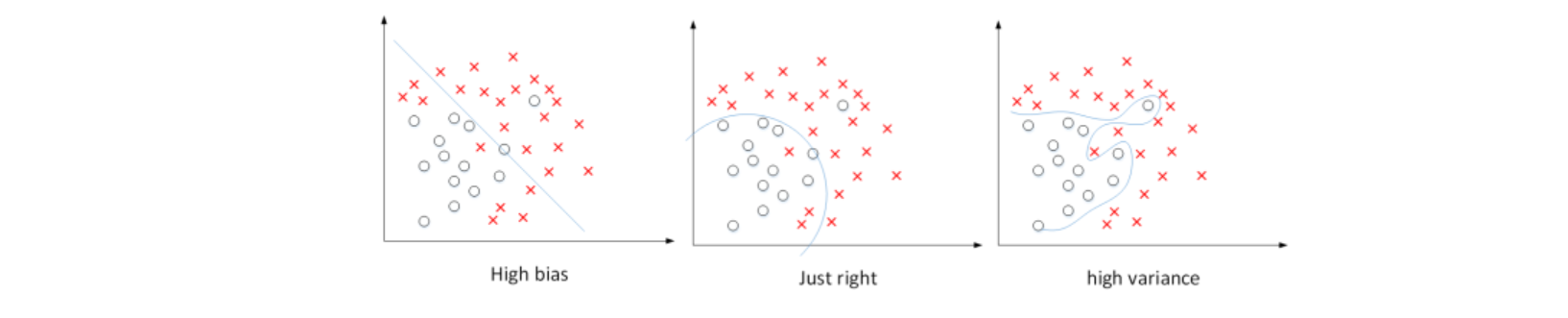
- 针对数据集,当使用简单模型(如逻辑回归)无法很好地拟合数据时,出现高偏差(high bias),即“欠拟合”(underfitting)。
- 相反,当使用过于复杂的模型(如深度神经网络)能够完美拟合数据,但泛化能力较差时,出现高方差(high variance),即“过拟合”(overfitting)。
- 介于过度拟合和欠拟合之间,存在一些适度拟合的模型,这种数据拟合看起来更加合理。
对于二维数据集,可以通过绘制数据和可视化分割边界来观察偏差和方差的情况。在多维空间数据中,虽无法直接绘制数据,但可以通过训练集误差和验证集误差研究偏差和方差。
训练集误差和验证集误差
- 关键数据包括训练集误差(Train set error)和验证集误差(Dev set error)。
- 通过比较训练集误差和验证集误差,可以诊断算法是否具有高方差或高偏差。
诊断算法的高偏差和高方差
我们以识别猫狗为例,人类都能正确识别所有猫类图片
即base error为0。base error不同,相应的Train set error和Dev set error会有所变化,但没有相对变化。,对于此种情况:

高方差:假设Train set error为1%,而Dev set error为11%,即该算法模型对训练样本的识别很好,但是对验证集的识别却不太好。这说明了该模型对训练样本可能存在过拟合,模型泛化能力不强,导致验证集识别率低。这恰恰是high variance的表现。训练集误差较低,但验证集误差较高,导致过度拟合。
高偏差:假设Train set error为15%,而Dev set error为16%,虽然二者error接近,即该算法模型对训练样本和验证集的识别都不是太好。这说明了该模型对训练样本存在欠拟合。这恰恰是high bias的表现。训练集误差和验证集误差都较高,导致欠拟合。
高偏差&高方差: 假设Train set error为15%,而Dev set error为30%,说明了该模型既存在high bias也存在high variance(深度学习中最坏的情况)。
低偏差&低方差: 再假设Train set error为0.5%,而Dev set error为1%,即low bias和low variance,是最好的情况。
高偏差&高方差的情况
一般来说,Train set error体现了是否出现bias,Dev set error体现了是否出现variance(正确地说,应该是Dev set error与Train set error的相对差值)。
我们已经通过二维平面展示了high bias或者high variance的模型,下图展示了high bias and high variance的模型: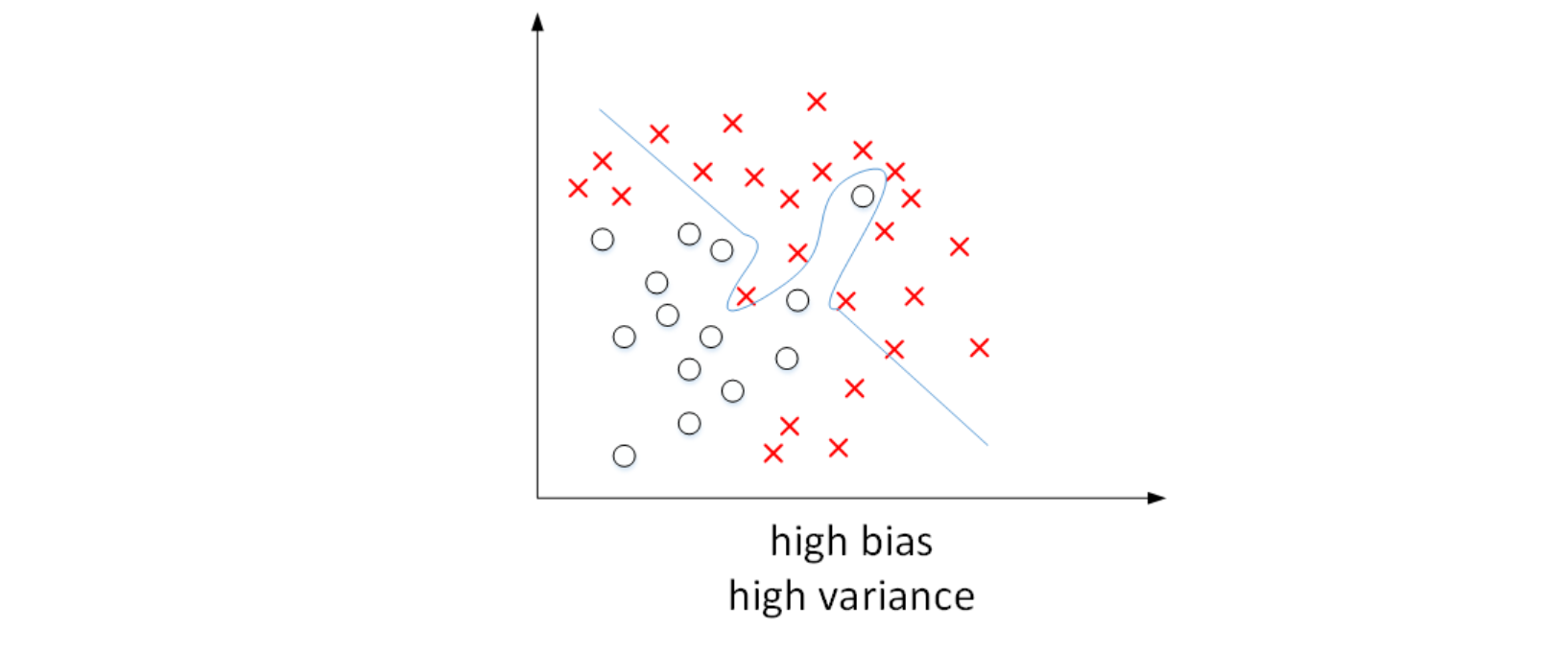
模型既存在high bias也存在high variance,可以理解成某段区域是欠拟合的,某段区域是过拟合的。
如何减小high bias和high variance
减少high bias :增加神经网络的隐藏层个数、神经元个数,训练时间延长,选择其它更复杂的NN模型等。
减少high variance :增加训练样本数据,进行正则化Regularization,选择其他更复杂的NN模型等
1.3 机器学习基础(Basic Recipe for Machine Learning)
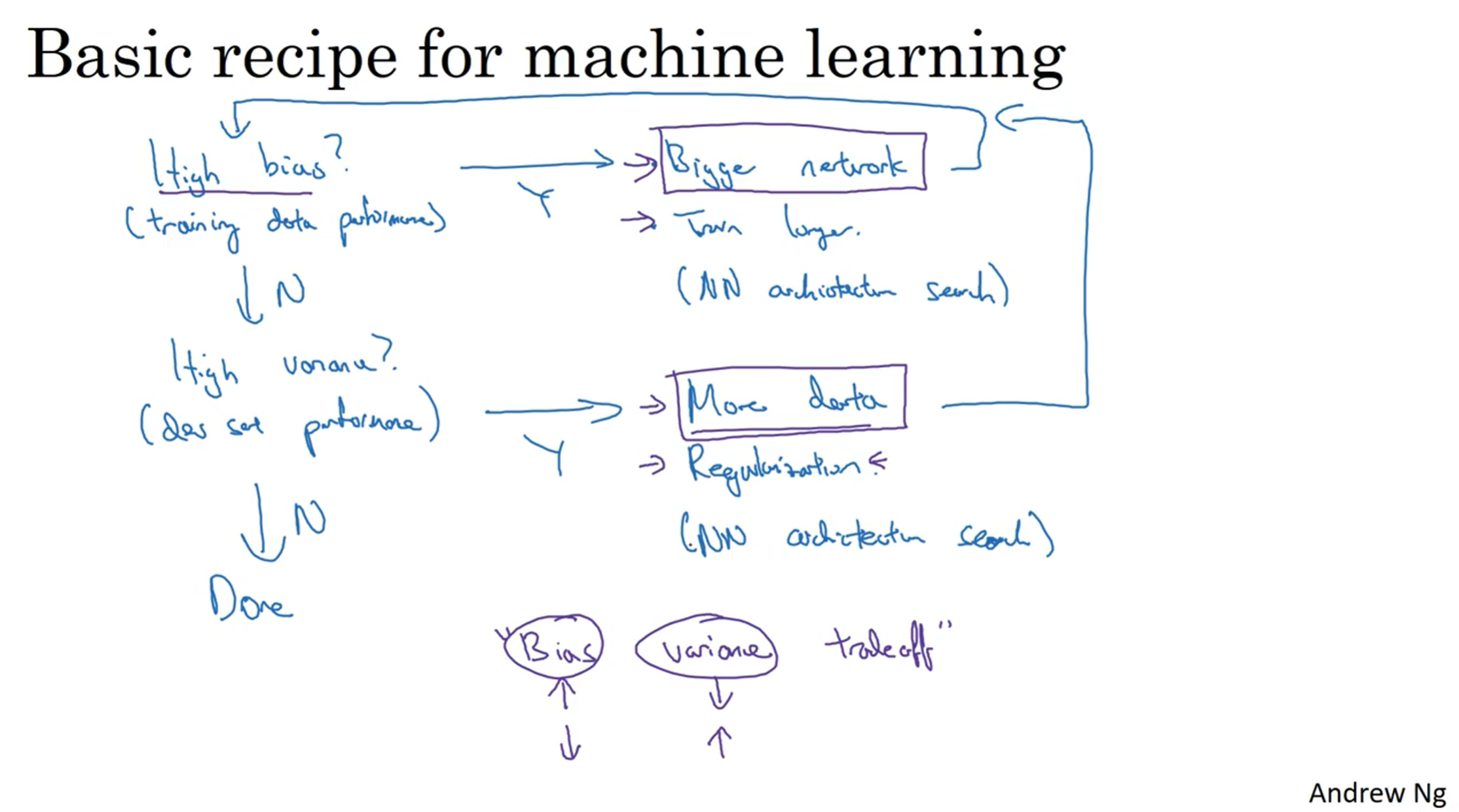
在训练神经网络时,我们需要考虑偏差(bias)和方差(variance)的问题。初始模型训练完成后,我们首先要评估算法的偏差水平。如果偏差较高,意味着模型无法很好地拟合训练集数据,可以选择一个新的网络架构,例如增加更多的隐藏层或隐藏单元,这样通常可以提升模型的拟合能力。另外,可以花费更多时间来训练网络,或者尝试使用更先进的优化算法。
一旦偏差降低到可接受的水平,我们需要检查方差的问题。如果方差较高,解决方案之一是增加更多的数据。然而,有时候我们无法获得更多的数据,这时我们可以尝试使用正则化方法来减少过拟合。
有时候,我们不得不反复尝试不同的方法。但是,如果能找到更合适的神经网络架构,有时候它可以同时减少偏差和方差。
1.4 正则化(Regularization)
如果出现了过拟合,可以通过扩大训练样本数量来减小方差,但是通常获得更多训练样本的成本太高,比较困难。所以,更可行有效的办法就是使用正则化(regularization)来解决。
常见正则化类型有L1正则化和L2正则化,其中L2正则化是最常用的。
L2 regularization
L2正则化采用矩阵范数的平方来衡量模型复杂度,将矩阵中所有元素的平方和作为正则化项,并乘以正则化参数λ和系数1/2m,加入到损失函数中,从而减小参数的值。将之前的Logistic regression采用L2 regularization 为:
$$\begin{gathered}J(w,b)=\frac1m\sum_{i=1}^mL(\hat{y}^{(i)},y^{(i)})+\frac\lambda{2m}||w||_2^2\||w||2^2=\sum{j=1}^{n_x}w_j^2=w^Tw\end{gathered}$$
在神经网络中应用L2正则化:
$$\begin{gathered}\begin{aligned}J(w^{[1]},b^{[1]},\cdots,w^{[L]},b^{[L]})&=\frac1m\sum_{i=1}^mL(\hat{y}^{(i)},y^{(i)})+\frac\lambda{2m}\sum_{l=1}^L||w^{[l]}||^2\\||w^{[l]}||^2&=\sum_{i=1}^{n^{[l]}}\sum_{j=1}^{n^{[l-1]}}(w_{ij}^{[l]})^2\end{aligned}\end{gathered}$$
神经网络含有一个成本函数,该函数包含所有参数,其中正则项为$\frac\lambda{2m}\sum_{l=1}^L||w^{[l]}||^2$,其中$L$是神经网络所含的层数。
由于加入了正则化项,梯度下降算法中的计算表达式需要做如下修改:
$$\begin{gathered}dw^{[l]}=dw_{before}^{[l]}+\frac\lambda mw^{[l]}\\w^{[l]}:=w^{[l]}-\alpha\cdot dw^{[l]}\end{gathered}$$
L2正则化也被称为“权重衰减(weight decay)”,因为它乘以一个系数$(1 - \alpha\frac{\lambda}{m})$来减小权重指标。不断迭代更新,不断地减小。
$$\begin{aligned}
w^{[l]}& :=w^{[l]}-\alpha\cdot dw^{[l]} \
&=w^{[l]}-\alpha\cdot(dw_{before}^{[l]}+\frac\lambda mw^{[l]}) \
&=(1-\alpha\frac\lambda m)w^{[l]}-\alpha\cdot dw_{before}^{[l]}
\end{aligned}$$
L1 regularization
$$\begin{gathered}J(w,b)=\frac1m\sum_{i=1}^mL(\hat{y}^{(i)},y^{(i)})+\frac\lambda{2m}||w||1\||w||1=\sum{j=1}^{nx}|w_j|\end{gathered}$$
使用L1正则化,正则项为$\frac{\lambda}{m}$乘以$\sum{j= 1}^{n_{x}}{|w|}$,其中$\sum_{j =1}^{n_{x}}{|w|}$也被称为参数$w$向量的L1范数。使用L1正则化后,$w$最终会是稀疏的,即$w$向量中有很多0,其优点是能够降低存储内存。
然而,实际上L1 regularization在解决high variance方面比L2 regularization并不更具优势。而且,L1的在微分求导方面比较复杂。所以,一般L2 regularization更加常用。
总结
正则化能够通过减小参数的值来降低模型的复杂度,从而防止过拟合的出现。
正则化的目的就是让权重w在一个约束范围内梯度下降并寻找最优解
1.5 为什么正则化有利于预防过拟合呢?(Why regularization reduces overfitting?)
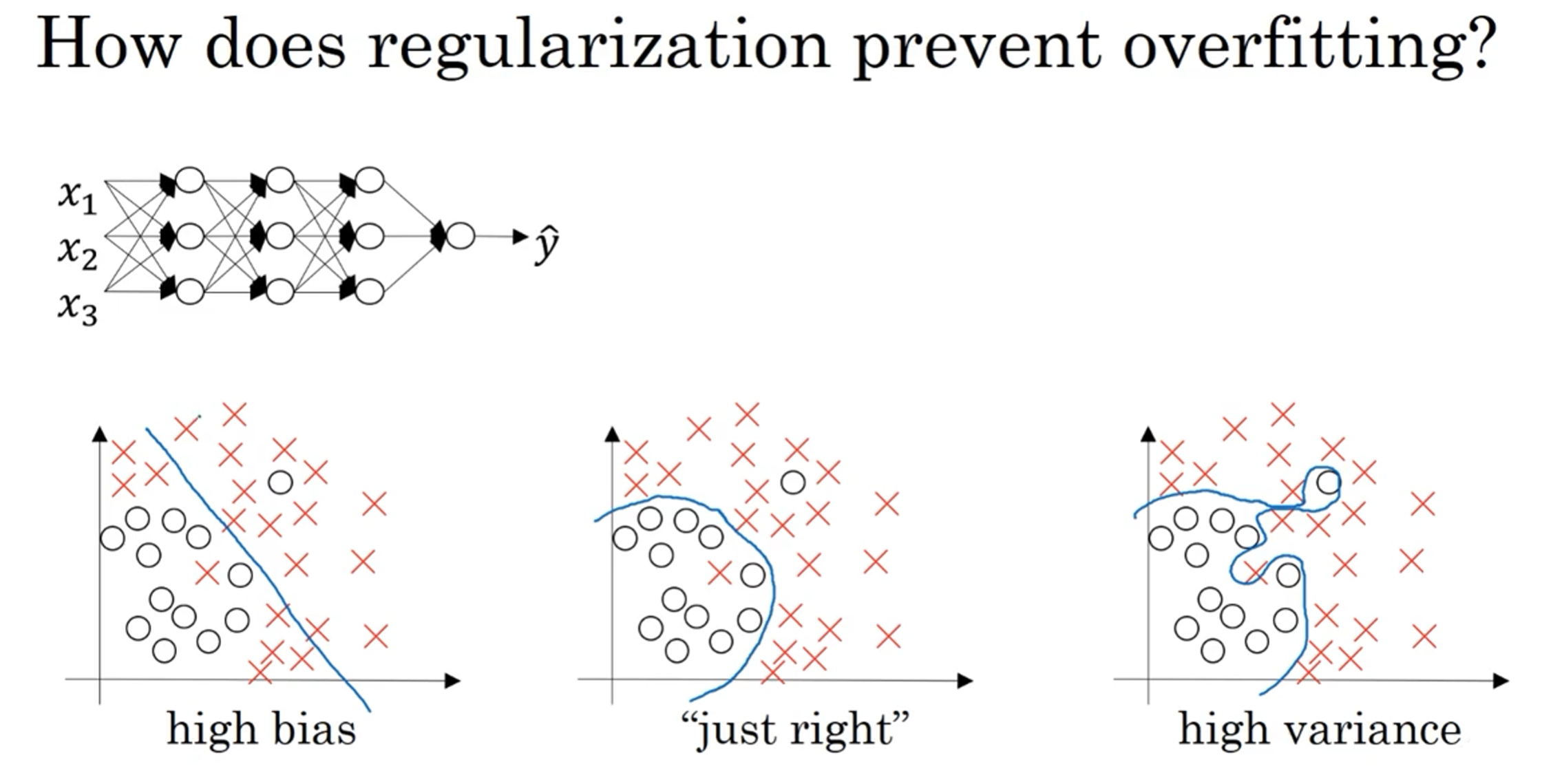
假如我们选择了非常复杂的神经网络模型,如上图左上角所示。在未使用正则化的情况下,我们得到的分类超平面可能是类似上图右侧的过拟合。但是,如果使用L2 regularization,当$\lambda$很大时,$w^{[l]}\approx0$。$w^{[l]}$近似为零,意味着该神经网络模型中的某些神经元实际的作用很小,可以忽略。
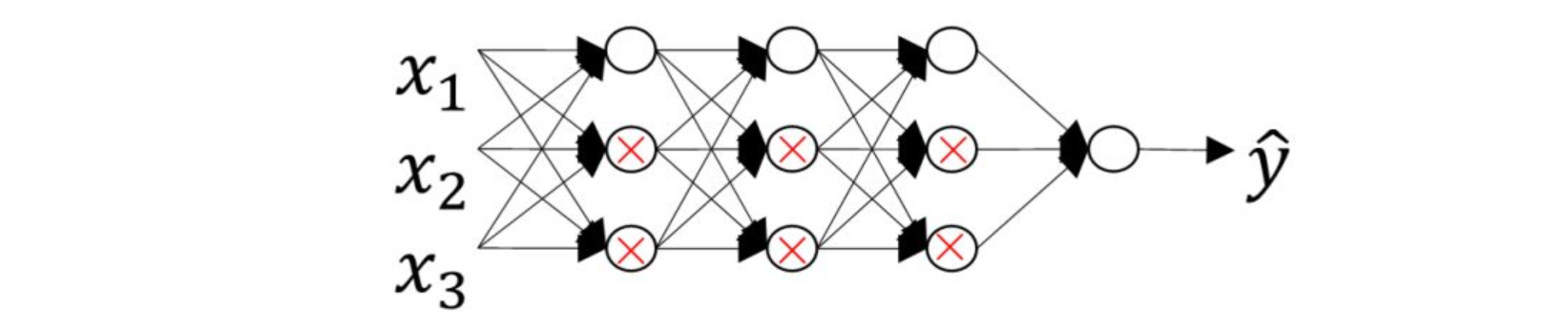
从效果上来看,其实是将某些神经元给忽略掉了。这样原本过于复杂的神经网络模型就变得不那么复杂了,而变得非常简单化了。如上图所示,整个简化的神经网络模型变成了一个逻辑回归模型。问题就从high variance变成了high bias 了。
还有另外一个直观的例子来解释为什么正则化能够避免发生过拟合。假设激活函数是tanh函数。tanh函数的特点是在z接近零的区域,函数近似是线性的,而当|z|很大的时候,函数非线性且变化缓慢。当使用正则化,$\lambda$较大,即对权重$w^{[l]}$的惩罚较大,$w^{[l]}$减小。因为$z^{[l]}=w^{[l]}a^{[l]}+b^{[l]}$,当$w^{[l]}$减小的时候,$z^{[l]}$也会减小。则此时的$z^{[l]}$分布在tanh函数的近似线性区域(下图红色部分)。那么这个神经元起的作用就相当于是linear regression。如果每个神经元对应的权重$w^{[l]}$都比较小,那么整个神经网络模型相当于是多个linear regression的组合,即可看成一个linear network。得到的分类超平面就会比较简单,不会出现过拟合现象。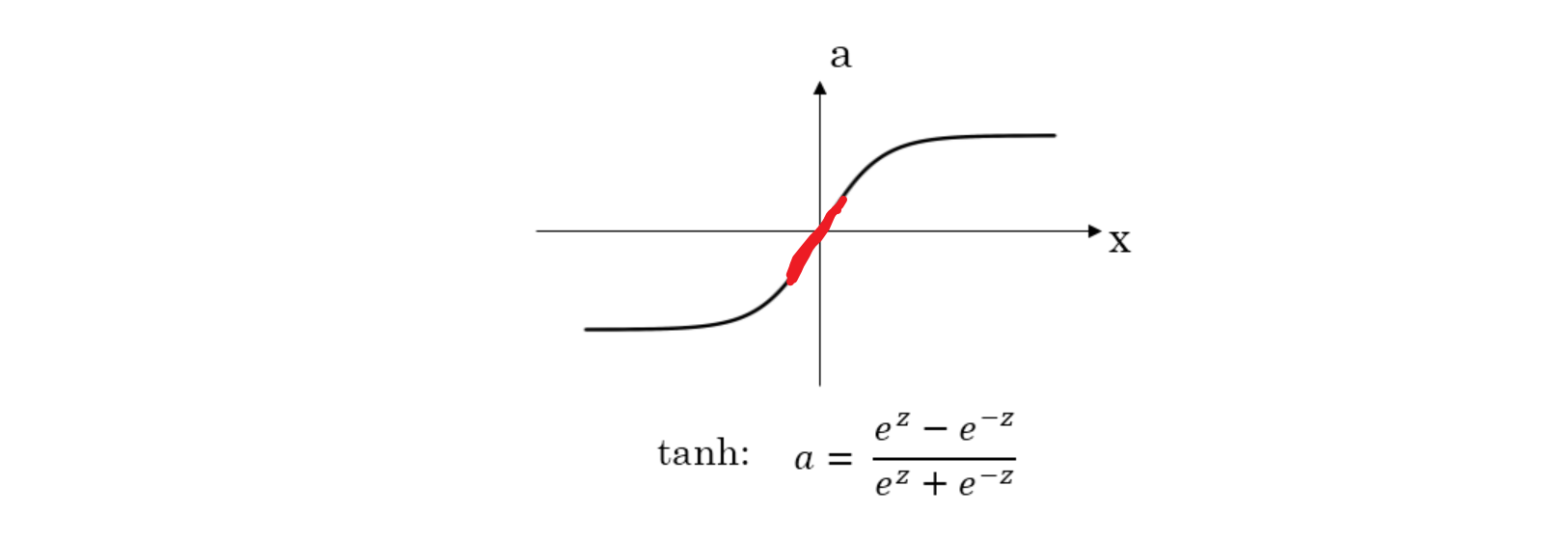
1.6 Dropout(Dropout)
除了L2 regularization之外,还有另外一种防止过拟合的有效方法:Dropout。
Dropout是指在深度学习网络的训练过程中,对于每层的神经元,按照一定的概率将其暂时从网络中丢弃。也就是说,每次训练时,每一层都有部分神经元不工作,起到简化复杂网络模型的效果,从而避免发生过拟合。
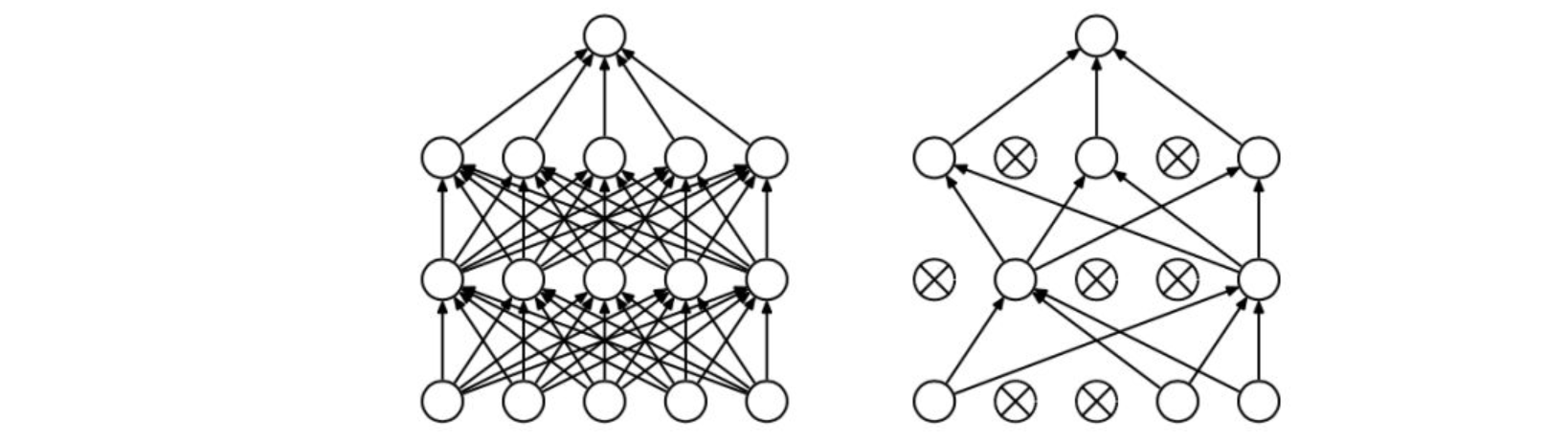
Dropout有不同的实现方法,接下来介绍一种常用的方法:Inverted dropout。
(1)假设对于第l层神经元,设定保留神经元比例概率keep_prob=0.8,即该层有20%的神经元停止工作。
(2)dl为dropout向量,设置dl为随机vector,其中80%的元素为1,20%的元素为0。在python中可以使用如下语句生成dropout vector:
1 | |
(3)然后,第l层经过dropout,随机删减20%的神经元,只保留80%的神经元,其输出为:
1 | |
(4)最后,还要对al进行scale up处理,即:
1 | |
以上就是Inverted dropout的方法。之所以要对al进行scale up是为了保证在经过dropout后,al作为下一层神经元的输入值尽量保持不变。
假设第l层有50个神经元,经过dropout后,有10个神经元停止工作,这样只有40个神经元有作用。
那么得到的al只相当于原来的80%,期望值小了20%。scale up后,能够尽可能保持al的期望值相比之前没有大的变化,不影响整体。
Inverted dropout的另外一个好处就是在对该dropout后的神经网络进行测试时能够减少scaling问题。
因为在训练时,使用scale up保证al的期望值没有大的变化,测试时就不需要再对样本数据进行类似的尺度伸缩操作了。
1.7 理解 dropout(Understanding Dropout)
Dropout基本概念
在每次迭代训练时,随机删除掉隐藏层一定数量的神经元;然后,在删除后的剩下的神经元上进行正向和反向更新权重w和常数项b;接着,下一次迭代中,再恢复之前删除的神经元,重新随机删除一定数量的神经元,进行正向和反向更新w和b。不断重复上述过程,直至迭代训练完成。
值得注意的是,使用dropout训练结束后,==在测试和实际应用模型时,不需要进行dropout和随机删减神经元==,所有的神经元都在工作。
Dropout防止过拟合的原理
Dropout通过每次迭代训练时,随机选择不同的神经元,相当于每次都在不同的神经网络上进行训练,类似机器学习中Bagging的方法,能够防止过拟合。
从权重w的角度解释防止过拟合的原理
对于某个神经元来说,某次训练时,它的某些输入在dropout的作用被过滤了。而在下一次训练时,又有不同的某些输入被过滤。经过多次训练后,某些输入被过滤,某些输入被保留。
这样,该神经元就不会受某个输入非常大的影响,影响被均匀化了。也就是说,对应的权重w不会很大。
这从效果上来说,与L2 regularization是类似的,都是对权重w进行“惩罚”,减小了w的值。
总的来说,对于同一组训练数据,利用不同的神经网络训练之后,求其输出的平均值可以减少过拟合。
Dropout就是利用这个原理,每次丢掉一定数量的隐藏层神经元,相当于在不同的神经网络上进行训练,这样就减少了神经元之间的依赖性,即每个神经元不能依赖于某几个其他的神经元(指层与层之间相连接的神经元),使神经网络更加能学习到与其他神经元之间的更加健壮robust的特征。
注意事项
首先,不同隐藏层的dropout系数keep_prob可以不同。一般来说,神经元越多的隐藏层,keep_out可以设置得小一些,例如0.5;神经元越少的隐藏层,keep_out可以设置的大一些,例如0.8,设置是1。
另外,实际应用中,不建议对输入层进行dropout,如果输入层维度很大,例如图片,那么可以设置dropout,但keep_out应设置的大一些,例如0.8,0.9。
总体来说,就是越容易出现overfitting的隐藏层,其keep_prob就设置的相对小一些。没有准确固定的做法,通常可以根据validation进行选择。
Dropout在电脑视觉CV领域应用比较广泛,因为输入层维度较大,而且没有足够多的样本数量。
值得注意的是dropout是一种regularization技巧,用来防止过拟合的,最好只在需要regularization的时候使用dropout。
使用dropout的时候,可以通过绘制cost function来进行debug,看看dropout是否正确执行。一般做法是,将所有层的keep_prob全设置为1,再绘制cost function,即涵盖所有神经元,看J是否单调下降。下一次迭代训练时,再将keep_prob设置为其它值。
1.8 其他正则化方法(Other regularization methods)
数据增强
除了L2 regularization和dropout regularization之外,还有其它减少过拟合的方法。
其中一种方法是增加训练样本数量。但是通常成本较高,难以获得额外的训练样本。但是,我们可以对已有的训练样本进行一些处理来“制造”出更多的样本,称为data augmentation。
例如图片识别问题中,可以对已有的图片进行水平翻转、任意角度旋转、缩放或扩大等等。
这些处理都能“制造”出新的训练样本。虽然这些是基于原有样本的,但是对增大训练样本数量还是有很有帮助的,不需要增加额外成本,却能起到防止过拟合的效果。
early stopping
一个神经网络模型随着迭代训练次数增加,train set error一般是单调减小的,而dev set error 先减小,之后又增大。
也就是说训练次数过多时,模型会对训练样本拟合的越来越好,但是对验证集拟合效果逐渐变差,即发生了过拟合。
因此,迭代训练次数不是越多越好,可以通过train set error和dev set error随着迭代次数的变化趋势,选择合适的迭代次数,即early stopping。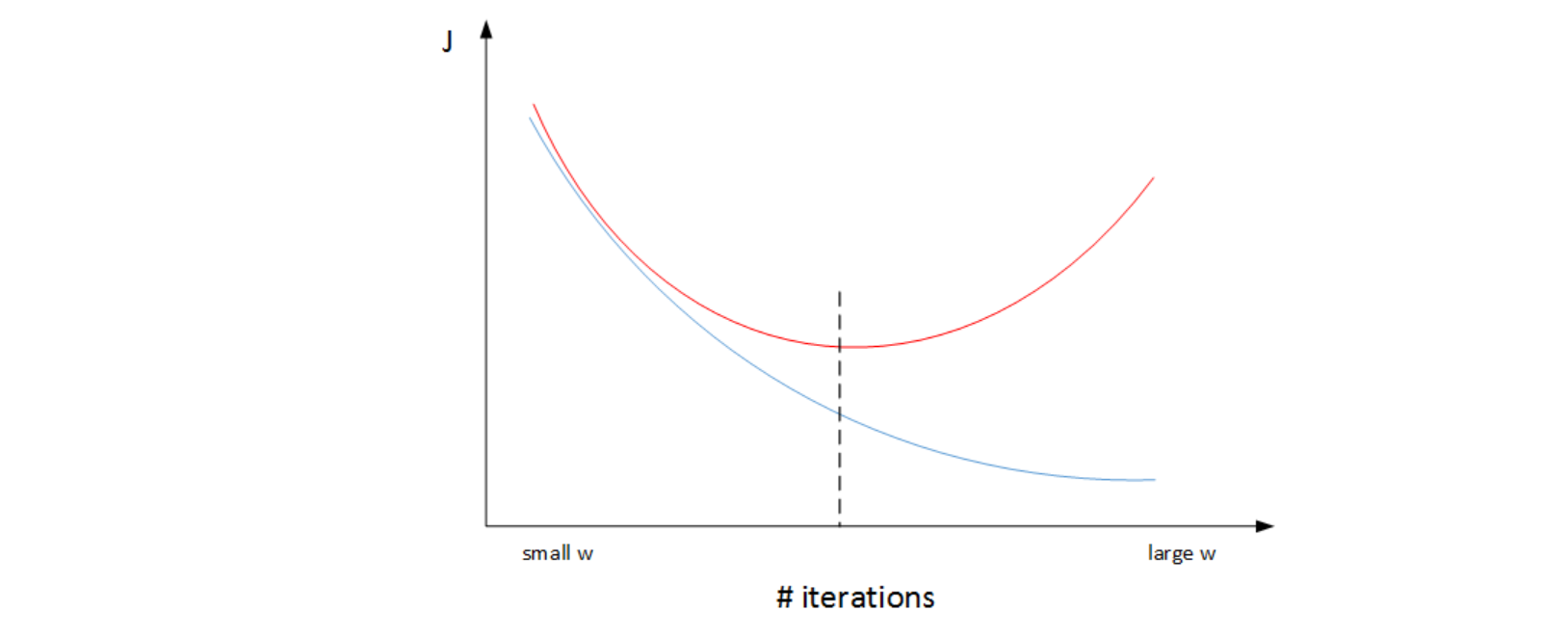
然而,Early stopping有其自身缺点。通常来说,机器学习训练模型有两个目标:一是优化cost function,尽量减小J;二是防止过拟合。
这两个目标彼此对立的,即减小J的同时可能会造成过拟合,反之亦然。我们把这二者之间的关系称为正交化orthogonalization。
在深度学习中,我们可以同时减小Bias和Variance,构建最佳神经网络模型。
但是,Early stopping的做法通过减少迭代次数来防止过拟合,这样J就不会足够小。也就是说,early stopping将上述两个目标融合在一起,同时优化,但可能没有“分而治之”的效果好。
与early stopping相比,L2 regularization可以实现“分而治之”的效果:迭代训练足够多,可以减小J,而且也能有效防止过拟合。
而L2 regularization的缺点之一是最优的正则化参数λ的选择比较复杂。
对这一点来说,early stopping比较简单。总的来说,L2 regularization更加常用一些。
1.9 归一化输入(Normalizing inputs)
在训练神经网络时,标准化输入可以提高训练的速度。标准化输入就是对训练数据集进行归一化的操作,即将原始数据减去其均值μ后,再除以其方差σ^2:
$$\begin{gathered}
\mu=\frac{1}{m}\sum_{i=1}^{m}X^{(i)} \
\sigma^{2}=\frac1m\sum_{i=1}^{m}(X^{(i)})^{2} \
\begin{aligned}X:=\frac{X-\mu}{\sigma^2}\end{aligned}
\end{gathered}$$
以二维平面为例,下图展示了其归一化过程:
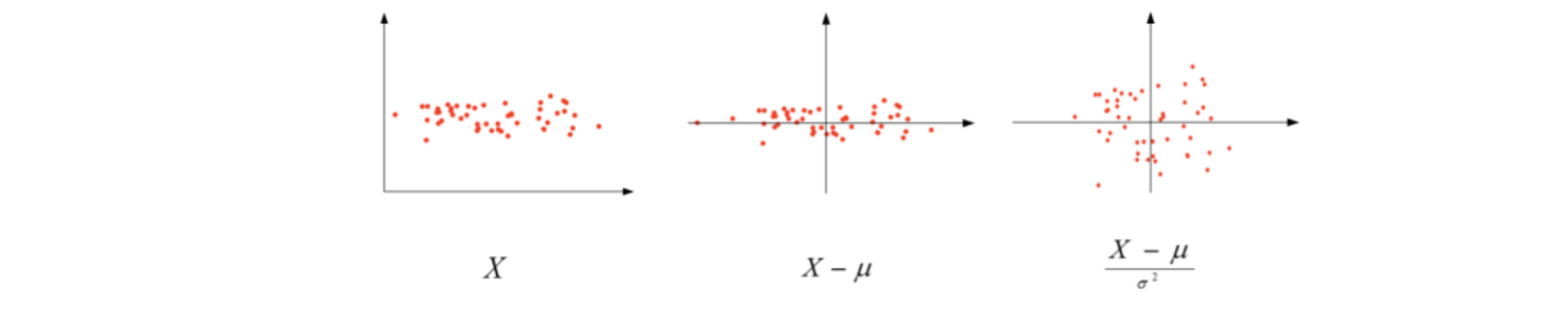
值得注意的是,由于训练集进行了标准化处理,那么对于测试集或在实际应用时,应该使用同样的μ和σ^2对其进行标准化处理。这样保证了训练集合测试集的标准化操作一致。
之所以要对输入进行标准化操作,主要是为了让所有输入归一化同样的尺度上,方便进行梯度下降算法时能够更快更准确地找到全局最优解。(原理可参考机器学习笔记->0监督学习->特征缩放)
1.10 梯度消失/梯度爆炸(Vanishing / Exploding gradients)
在神经网络尤其是深度神经网络中存在可能存在这样一个问题:梯度消失和梯度爆炸。
意思是当训练一个层数非常多的神经网络时,计算得到的梯度可能非常小或非常大,甚至是指数级别的减小或增大。这样会让训练过程变得非常困难。

为了简化复杂度,便于分析,我们令各层的激活函数为线性函数,即$g(Z)=Z$。且忽略各层常数项b的影响,令b全部为零。那么,该网络的预测输出$\hat{Y}$为:
$\hat{Y}=W^{[L]}W^{[L-1]}W^{[L-2]}\ldots W^{[3]}W^{[2]}W^{[1]}X$
如果各层权重$W^{[l]}$的元素都稍大于1,例如1.5, 则预测输出$\hat{Y}$将正比于$1.5^L$。L越大,$\hat{Y}$越大,且呈指数型增长。我们称之为数值爆炸。
相反,如果各层权重$W^{[l]}$的元素都稍小于1,例如0.5,则预测输出$\hat{Y}$将正比于$0.5^L$。网络层数L越多,$\hat{Y}$呈指数型减小。我们称之为数值消失。
也就是说,如果各层权重$W^{[l]}$都大于1或者都小于1,那么各层激活函数的输出将随着层数$l$的增加,呈指数型增大或减小。当层数很大时,出现数值爆炸或消失。同样,这种情况也会引起梯度呈现同样的指数型增大或减小的变化。L非常大时,例如L=150,则梯度会非常大或非常小,引起每次更新的步进长度过大或者过小,这让训练变得十分困难。
1.11 神经网络的权重初始化(Weight Initialization for Deep NetworksVanishing /Exploding gradients)
下面介绍如何改善梯度消失/梯度爆炸这类问题,方法是对权重w进行一些初始化处理。
如果激活函数是tanh,在初始化w时,令其方差为1/n。相应的python伪代码为:
1 | |
如果激活函数是ReLU,权重w的初始化一般令其方差为2/n:
1 | |
除此之外,Yoshua Bengio提出了另外一种初始Bengio提出了另外一种初始化w的方法,令其方差为:$\frac2{n^{[l-1]}n^{[l]}}$
1 | |
1.12 梯度检验(Gradient checking)
Back Propagation神经网络有一项重要的测试是梯度检查(gradient checking)。其目的是检查验证反向传播过程中梯度下降算法是否正确。
梯度的数值逼近
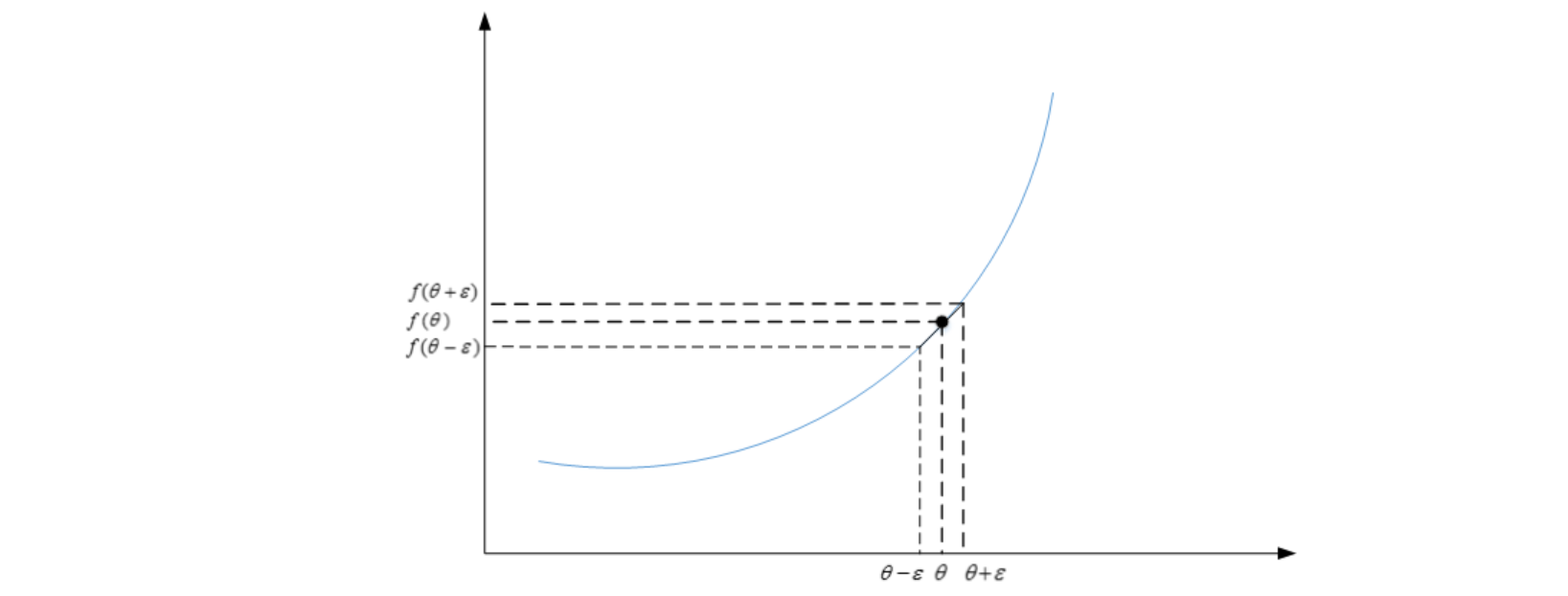
利用微分思想(中值定理$f(x)=(f(b)-f(a))/(b-a)$),函数f在点θ处的梯度可以表示成:
$$g(\theta)=\frac{f(\theta+\varepsilon)-f(\theta-\varepsilon)}{2\varepsilon}$$
其中,ε>0,且足够小。
函数f在点θ处的梯度近似等于$g(\theta)$的值。
梯度检验
用函数值去估计梯度,然后和记录下来的dw或者db比较,看是不是算对了
梯度检查首先要做的是分别将$W^{[1]},b^{[1]},\cdots,W^{[L]},b^{[L]}$这些矩阵构造成一维向量,然后将这些一维向量组合起来构成一个更大的一维 向 量 $\theta$。这 样 cost function $J(W^{[1]},b^{[1]},\ldots,W^{[L]},b^{[L]})$ 就 可以表示成$J(\theta)$。
然后将反向传播过程通过梯度下降算法得到的
$dW^{[1]},db^{[1]},\cdots,dW^{[L]},db^{[L]}$按照一样的顺序构造成一个一维向量$d\theta$。$d\theta$的维度与$\theta$一致。
接着利用$J(\theta)$对每个$\theta_i$计算近似梯度,其值与反
向传播算法得到的$d\theta_i$相比较,检查是否一致。例如,对于第i个元素,近似梯度为:
$$d\theta_{approx}[i]=\frac{J(\theta_1,\theta_2,\cdots,\theta_i+\varepsilon,\cdots)-J(\theta_1,\theta_2,\cdots,\theta_i-\varepsilon,\cdots)}{2\varepsilon}$$
计算完所有$\theta_i$的近似梯度后,可以计算$d\theta_{approx}$与$d\theta$的欧氏(Euclidean) 距离来比较二者的相似度。公式如下:
$$\frac{||d\theta_{approx}-d\theta||2}{||d\theta{approx}||_2+||d\theta||_2}$$
一般来说,如果欧氏距离越小,例如$10^{-7}$,甚至更小,则表明$d\theta_{approx}$与$d\theta$越接近,即反向梯度计算是正确的,没有bugs。
如果欧氏距离较大, 例如$10^{-5}$,则表明梯度计算可能出现问题,需要再次检查是否有bugs存在。
如果欧氏距离很大,例如$10^{-3}$,甚至更大,则表明$d\theta_{approx}$与$d\theta$差别很大,梯度下降计算过程有bugs,需要仔细检查。
梯度检验应用的注意事项
不要在整个训练过程中都进行梯度检查,仅仅作为debug使用。
如果梯度检查出现错误,找到对应出错的梯度,检查其推导是否出现错误。
注意不要忽略正则化项,计算近似梯度的时候要包括进去。
梯度检查时关闭dropout,检查完毕后再打开dropout。
随机初始化时运行梯度检查,经过一些训练后再进行梯度检查(不常用)。