深度学习-Course1_Week4深层神经网络
1 深层神经网络
深层神经网络其实就是包含更多的隐藏层神经网络。
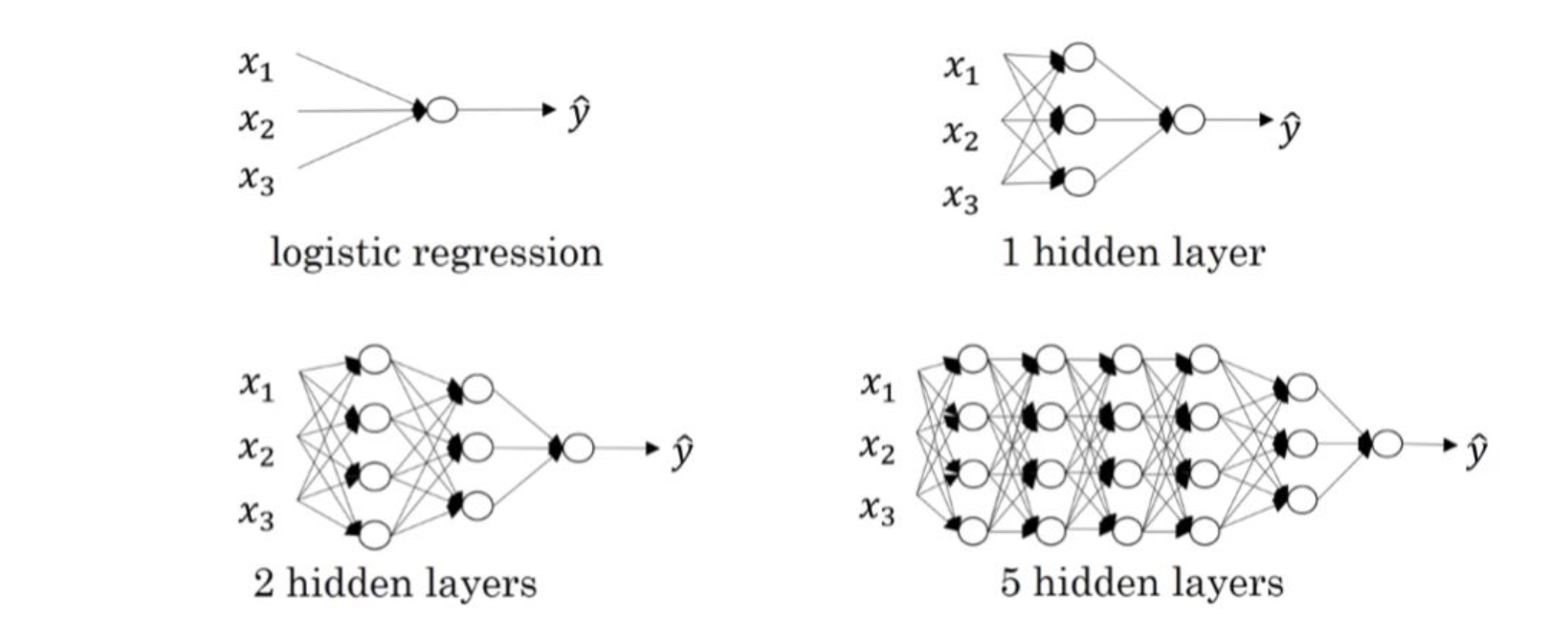
2 深层神经网络正向传播
接下来,我们来推导一下深层神经网络的正向传播过程。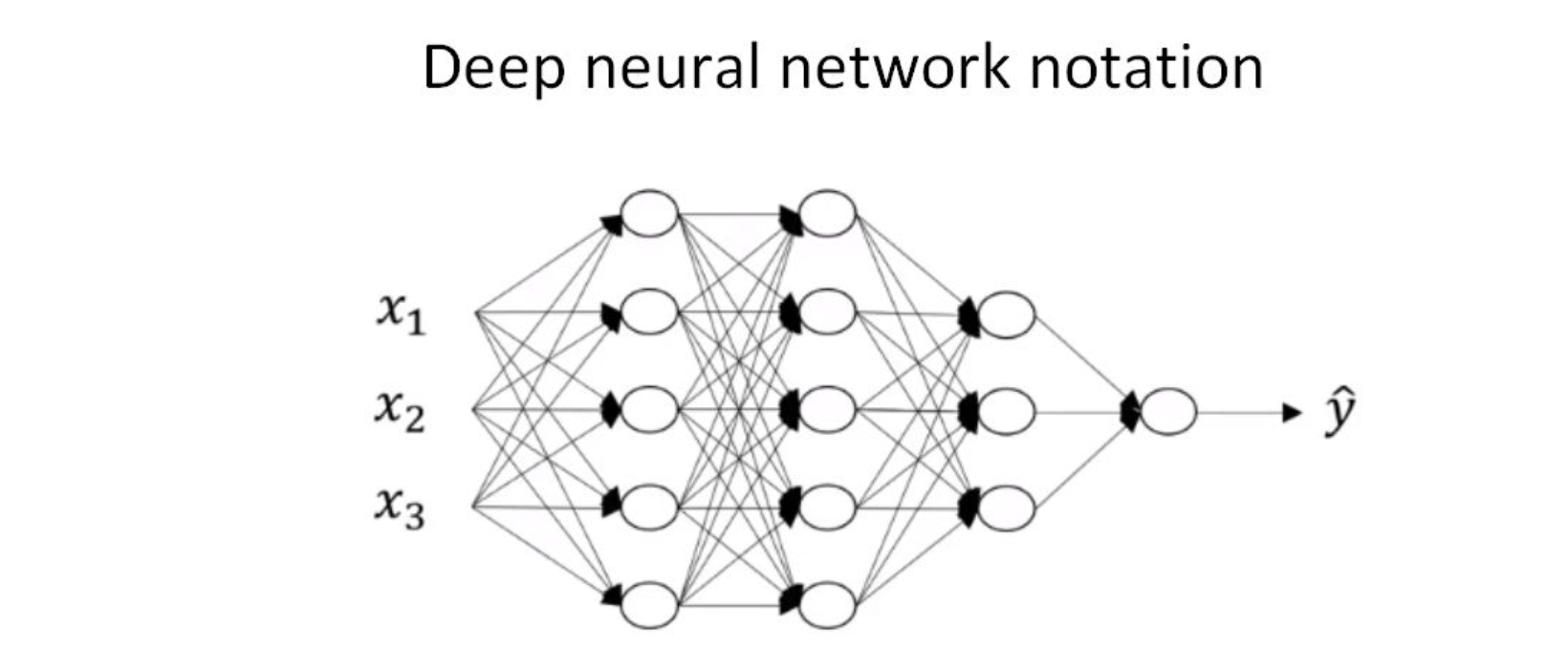
以4层神经网络为例,对于单个样本。
第1层,l=1:
$$\begin{gathered}z^{[1]}=W^{[1]}x+b^{[1]}=W^{[1]}a^{[0]}+b^{[1]}\a^{[1]}=g^{[1]}(z^{[1]})\end{gathered}$$
第2层,l=2:
$$\begin{gathered}z^{[2]}=W^{[2]}a^{[1]}+b^{[2]}\a^{[2]}=g^{[2]}(z^{[2]})\end{gathered}$$
第3层,l=3:
$$\begin{gathered}z^{[3]}=W^{[3]}a^{[2]}+b^{[3]}\a^{[3]}=g^{[3]}(z^{[3]})\end{gathered}$$
第4层,l=4:
$$\begin{gathered}z^{[4]}=W^{[4]}a^{[3]}+b^{[4]}\a^{[4]}=g^{[4]}(z^{[4]})\end{gathered}$$
如果有m个训练样本,其向量化矩阵形式为:
第1层,l=1:
$$\begin{gathered}Z^{[1]}=W^{[1]}X+b^{[1]}=W^{[1]}A^{[0]}+b^{[1]}\A^{[1]}=g^{[1]}(Z^{[1]})\end{gathered}$$
第2层,l=2:
$$\begin{gathered}Z^{[2]}=W^{[2]}A^{[1]}+b^{[2]}\A^{[2]}=g^{[2]}(Z^{[2]})\end{gathered}$$
第3层,l=3:
$$\begin{gathered}Z^{[3]}=W^{[3]}A^{[2]}+b^{[3]}\A^{[3]}=g^{[3]}(Z^{[3]})\end{gathered}$$
第4层,l=4:
$$\begin{gathered}Z^{[4]}=W^{[4]}A^{[3]}+b^{[4]}\A^{[4]}=g^{[4]}(Z^{[4]})\end{gathered}$$
因此,向前传播:
公式:
$$\begin{array}{c}\mathrm{z^{[l]}=W^{[l]}\cdot a^{[l-1]}+b^{[l]}}\\mathrm{a^{[l]}=g^{[l]}(z^{[l]})}\end{array}$$向量化:
$$\begin{gathered}Z^{[l]}=W^{[l]}A^{[l-1]}+b^{[l]}\A^{[l]}=g^{[l]}(Z^{[l]})\end{gathered}$$
其中l=1,⋯,L
3 正确处理矩阵维度
单个训练样本
对于单个训练样本,输入x的维度是( $n^{[0]},1$ )
参数$W^{[l]}$和$b^{[l]}$的维度分别是 :
$$\begin{gathered}W^{[l]}:(n^{[l]},n^{[l-1]})\b^{[l]}:(n^{[l]},1)\end{gathered}$$
反向传播过程中的$dW^{[l]}$和$db^{[l]}$的维度分别是:
$$\begin{gathered}dW^{[l]}:(n^{[l]},n^{[l-1]})\db^{[l]}:(n^{[l]},1)\end{gathered}$$
正向传播过程中的$z^{[l]}$和$a^{[l]}$的维度分别是:
$$\begin{aligned}z^{[l]}&:&(n^{[l]},1)\a^{[l]}&:&(n^{[l]},1)\end{aligned}$$
m个训练样本
对于m个训练样本,输入矩阵X的维度是( $n^{[0]},m$ )。
$W^{[l]}$和$b^{[l]}$的维度与只有单个样本是一致的:
$$\begin{gathered}W^{[l]}:(n^{[l]},n^{[l-1]})\b^{[l]}:(n^{[l]},1)\end{gathered}$$
$dW^{[l]}$和$db^{[l]}$的维度分别与$W^{[l]}$和$b^{[l]}$的相同
$Z^{[l]}$和$A^{[l]}$的维度分别是:
$$\begin{aligned}Z^{[l]}&:&(n^{[l]},m)\A^{[l]}&:&(n^{[l]},m)\end{aligned}$$
$dZ^{[l]}$ 和 $dA^{[l]}$的维度分别与$Z^{[l]}$和$A^{[l]}$的相同
5 深层神经网络流程块
下面用流程块图来解释神经网络正向传播和反向传播过程。如下图所示,对于第l层来说,正向传播过程中:
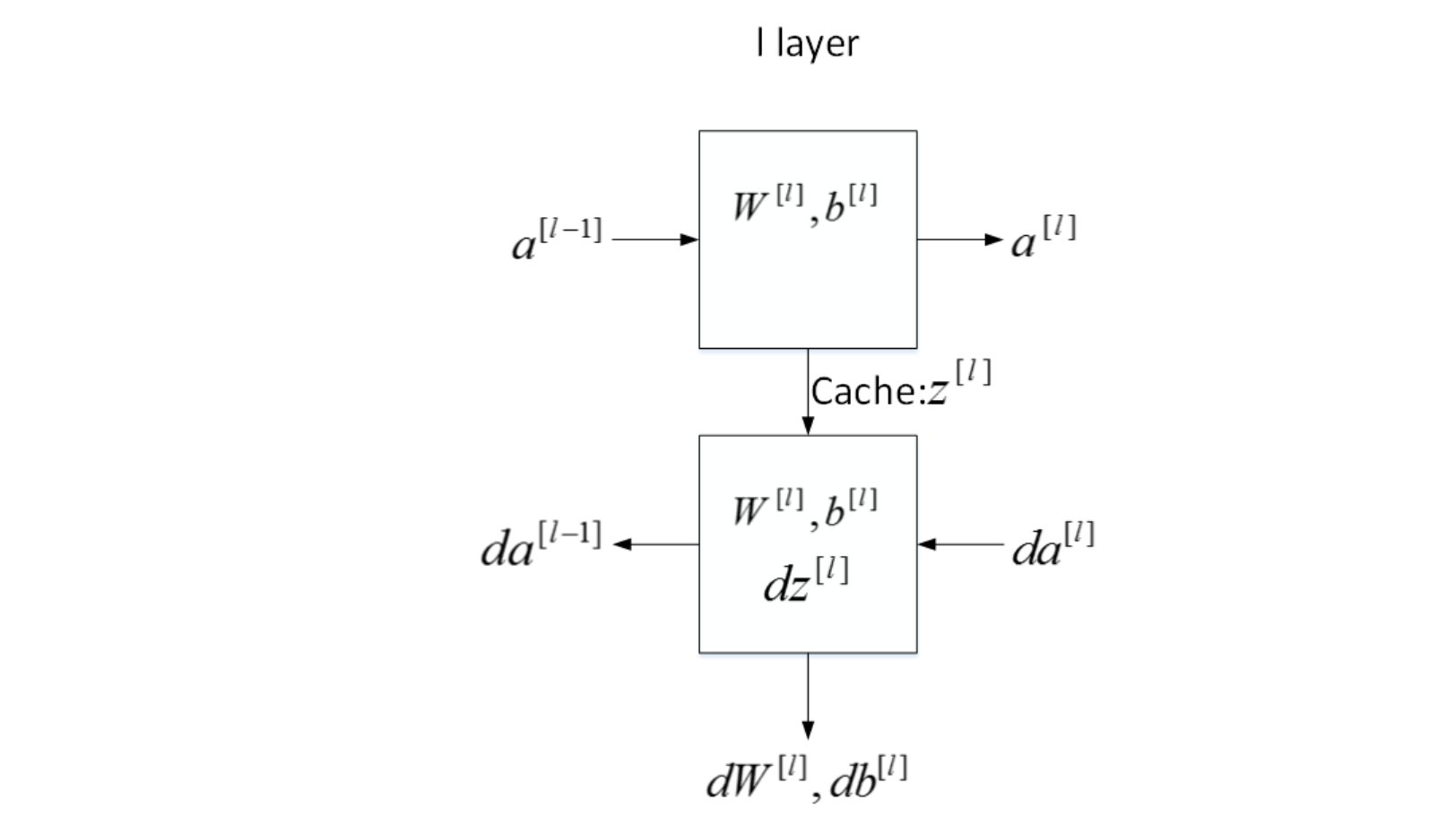
这是第l层的流程块图,对于神经网络所有层,整体的流程块图正向传播过程和反向传播过程如下所示: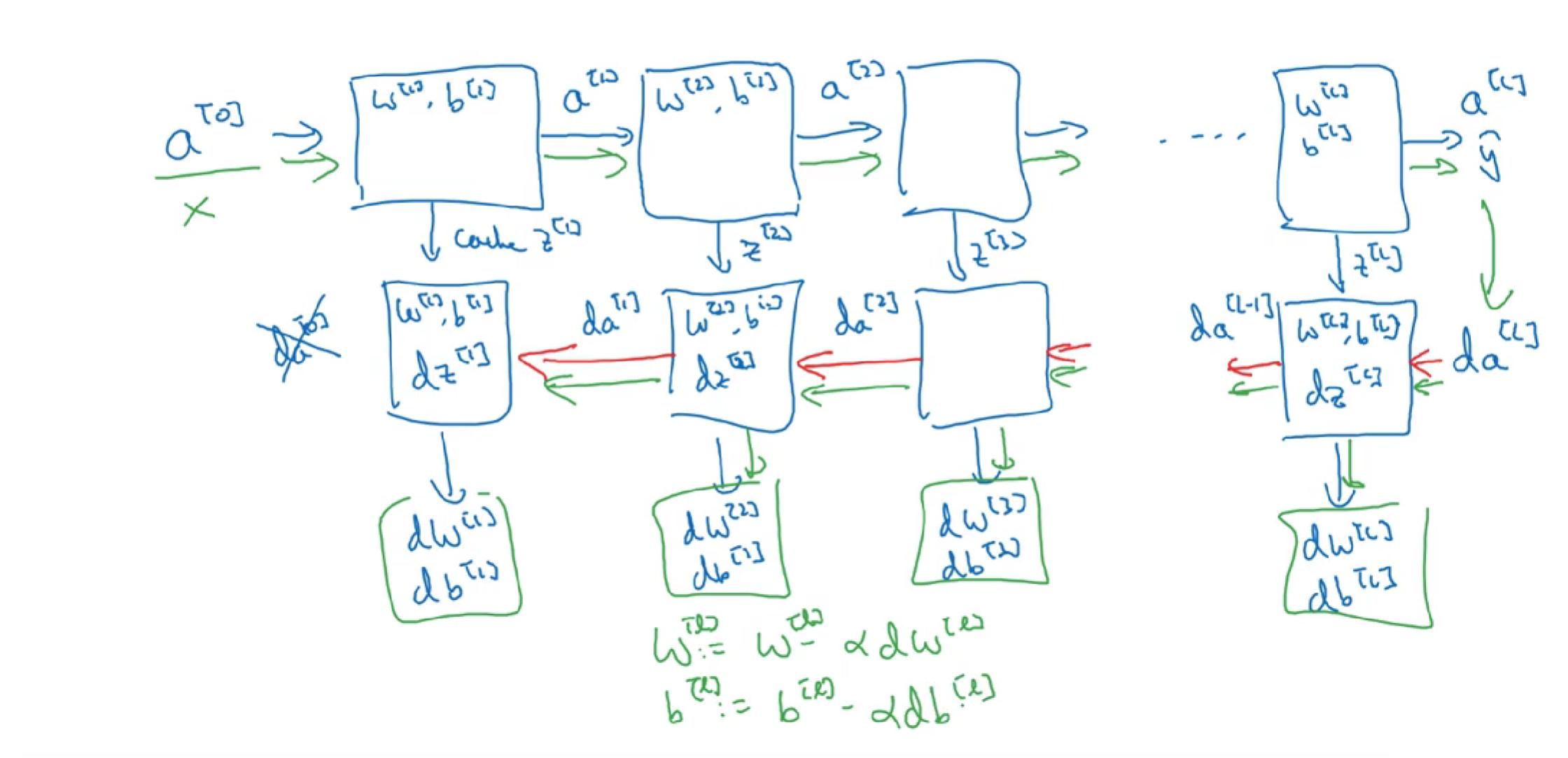
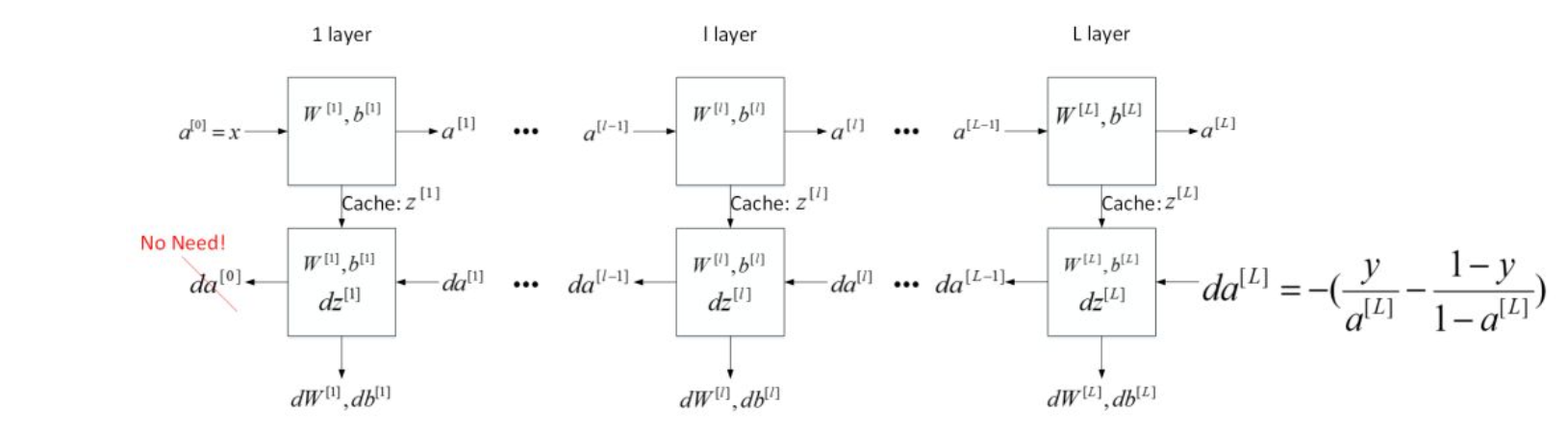
6 前向传播和反向传播
之前我们学习了构成深度神经网络的基本模块,比如每一层都有前向传播步骤以及一个相反的反向传播步骤,这次视频我们讲讲如何实现这些步骤。
先讲前向传播,输入$a^{[l-1]}$,输出是$a^{[l]}$,缓存为$z^{[l]}$;从实现的角度来说我们可以缓存下$w^{[l]}$和$b^{[l]}$,这样更容易在不同的环节中调用函数。
所以前向传播的步骤为:
$z^{[l]}=W^{[l]}\cdot a^{[l-1]}+b^{[l]}$
$a^{[l]}=g^{[l]}(z^{[l]})$
向量化实现过程为:
$Z^{[l]}=W^{[l]}\cdot A^{[l-1]}+b^{[l]}$
$A^{[l]}=g^{[l]}(Z^{[l]})$
前向传播需要输入$A^{[0]}$也就是$X$,来初始化;初始化的是第一层的输入值。$a^{[0]}$对应于一个训练样本的输入特征,而$A^{[0]}$对应于一整个训练样本的输入特征,所以这就是这条链的第一个前向函数的输入,重复这个步骤就可以从左到右计算前向传播。
下面讲反向传播的步骤:
输入为$da^{[l]}$,输出为$da^{[l-1]}$,$dw^{[l]}$,$db^{[l]}$

反向传播的步骤为:
(1) $d{ {z}^{[l]} }=d{ {a}^{[l]} }*{ {g}^{[l]} }’( { {z}^{[l]} })$
(2) $d{ {w}^{[l]} }=d{ {z}^{[l]} }\cdot{ {a}^{[l-1]} }~$
(3) $d{ {b}^{[l]} }=d{ {z}^{[l]} }~~$
(4) $d{ {a}^{[l-1]} }={ {w}^{\left[ l \right]T} }\cdot { {dz}^{[l]} }$
(5) $d{ {z}^{[l]} }={ {w}^{[l+1]T} }d{ {z}^{[l+1]} }\cdot \text{ }{ {g}^{[l]} }’( { {z}^{[l]} })~$
式子(5)由式子(4)带入式子(1)得到,前四个式子就可实现反向函数。
向量化实现过程为:
(6) $d{ {Z}^{[l]} }=d{ {A}^{[l]} }*{ {g}^{\left[ l \right]} }’\left({ {Z}^{[l]} } \right)~~$
(7) $d{ {W}^{[l]} }=\frac{1}{m}\text{}d{ {Z}^{[l]} }\cdot { {A}^{\left[ l-1 \right]T} }$
(8) $d{ {b}^{[l]} }=\frac{1}{m}\text{ }np.sum(d{ {z}^{[l]} },axis=1,keepdims=True)$
(9) $d{ {A}^{[l-1]} }={ {W}^{\left[ l \right]T} }.d{ {Z}^{[l]} }$
总结: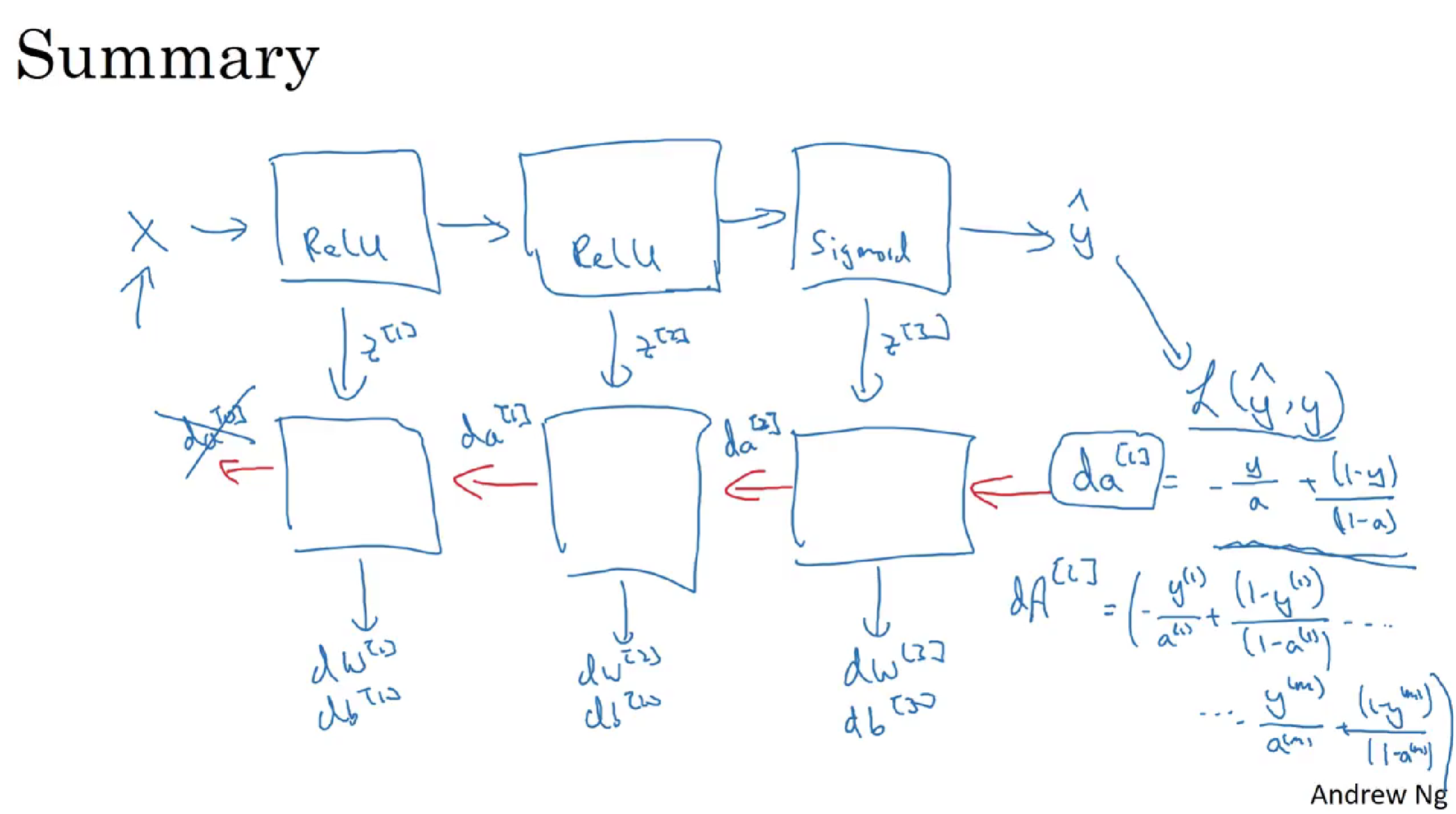
7 神经网络参数和超参数
神经网络中的参数(parameters)就是我们熟悉的$W^{[l]}$和$b^{[l]}$。而超参数(hyperparameters)则是例如学习速率$\alpha$,训练迭代次数 N,神经网络层数L,各层神经元个数$n^{[l]}$,激活函数$g(z)$等。之所以叫做超参数的原因是它们决定了参数$W^{[l]}$和$b^{[l]}$的值。