C语言03-函数和递归123

1 函数分类

1.1 库函数

库函数查询工具：
www.cplusplus.com
http://en.cppreference.com（英文版）
http://zh.cppreference.com（中文版）

1.2 自定义函数

ret_type fun_name(para1, * )
{
	statement;//语句项
}

ret_type 返回类型
fun_name 函数名
para1 函数参数

写一个函数可以交换两个整形变量的内容。P12 1:16:10

#include <stdio.h>
//实现成函数，但是不能完成任务
void Swap1(int x, int y)
{
	int tmp = 0;
	tmp = x;
	x = y;
	y = tmp;
}
// x y 和 num1 num2是单独的地址，没有关系

//正确的版本
void Swap2(int* px, int* py)
{
	int tmp = 0;
	tmp = *px;
	*px = *py;
	*py = tmp;
}
int main()
{
	int num1 = 1;
	int num2 = 2;
	Swap1(num1, num2);
	printf("Swap1:num1 = %d num2 = %d\n", num1, num2);
	Swap2(&num1, &num2);
	printf("Swap2:num1 = %d num2 = %d\n", num1, num2);
	return 0;
}

2 函数的参数

2.1 实参

真实传给函数的参数，叫实参。
实参可以是：常量、变量、表达式、函数等。
无论实参是何种类型的量，在进行函数调用时，它们都必须有确定的值，以便把这些值传送给形
参。

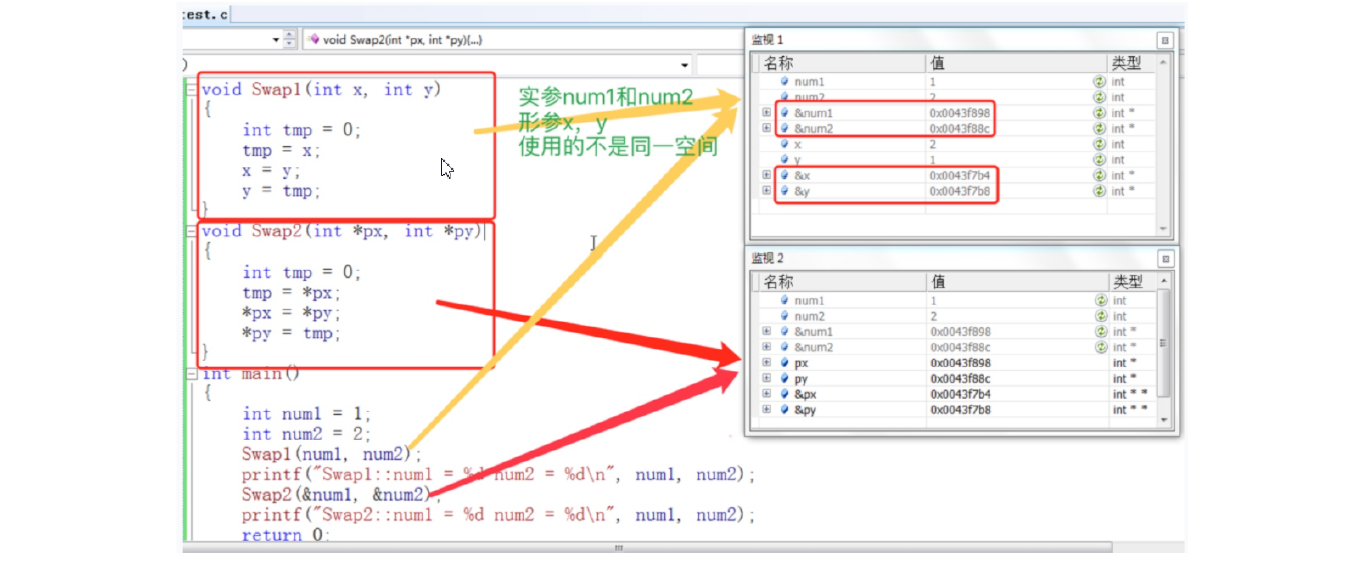
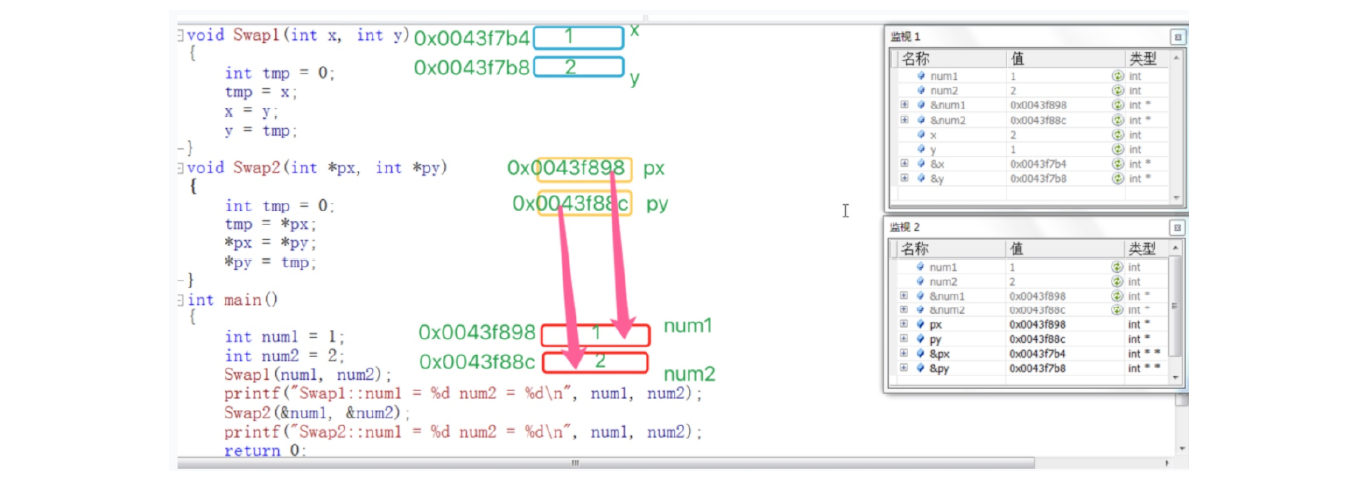
2.2 形参

形式参数是指函数名后括号中的变量，因为形式参数只有在函数被调用的过程中才实例化（分配内
存单元），所以叫形式参数。形式参数当函数调用完成之后就自动销毁了。因此形式参数只在函数
中有效。
上面Swap1 和Swap2 函数中的参数x，y，px，py 都是形式参数。
在main函数中传给Swap1 的num1 ， num2 和传给Swap2 函数的&num1 ， &num2 是实际参数。
这里我们对函数的实参和形参进行分析：

代码对应的内存分配如下：

这里可以看到Swap1 函数在调用的时候， x ， y 拥有自己的空间，同时拥有了和实参一模一样的内容。
当实参传给形参的时候，形参其实是实参的一份临时搓贝
，对形参的修改是不会改变实参的。

3 函数的调用

3.1 传值调用

函数的形参和实参分别占有不同内存块，对形参的修改不会影响实参。

3.2 传址调用

传址调用把变量的内存地址传递给函数参数。
这种传参方式可以让函数和函数外边的变量建立起真正的联系，也就是函数内部可以直接操作函数外部的变量。

3.3 练习

// 写一个函数，实现一个整形有序数组的二分查找。
// 找到返回下标。未找到返回-1

int binarySearch(int arr[],int n,int size)
{
	
	int left = 0;
	int right = size - 1;
	int mind = 0;

	while (left<=right)
	{
		mind = (left + right) / 2;
		if (arr[mind] < n)
		{
			left = mind+1;
		}
		else if (arr[mind] > n)
		{
			right = mind-1;
		}
		else
		{
			return mind;
		}
	}
	return -1;
}

int main()
{	
	int arr[] = {1,2,3,4,5};
	int n = 2;
	int size = (sizeof(arr) / sizeof(arr[0]));
	int index = binarySearch(arr,n,size);
	if (-1 != index)
	{
		printf("找到了，下标为：%d\n", index);
	}
	else
		printf("没找到");
	return 0;
}

注意： int size = (sizeof(arr) / sizeof(arr[0])); 要写在函数外。mind = (left + right) / 2; 要写在循环内。

// 写一个函数，每调用一次这个函数，就会将num 的值增加1。

void Add(int* p)
{
	(*p)++;
}

int main()
{
	int num = 0;
	Add(&num);
	printf("num = %d\n", num);
	Add(&num);
	printf("num = %d\n", num);
	Add(&num);
	printf("num = %d\n", num);
	return 0;
}

注意：(*p)++; 不可写成 *p++ ，因为++ 级别较高 *p++ 的话 ++ 是作用在 p 上的，不是作用在 *P 上的。

4 函数的嵌套调用和链式访问

4.1 嵌套调用

#include <stdio.h>
void new_line()
{
	printf("hehe\n");
}
void three_line()
{
	int i = 0;
	for(i=0; i<3; i++)
	{
		new_line();
	}
}
int main()
{
	three_line();
	return 0;
}

4.2 链式访问

把一个函数的返回值作为另外一个函数的参数。

#include <stdio.h>
int main()
{
	printf("%d", printf("%d", printf("%d", 43)));
	return 0;
}

结果：4321
注意：printf函数的返回值是打印在屏幕上字符的个数

5 函数的声明和定义

5.1 函数的声明

1. 告诉编译器有一个函数叫什么，参数是什么，返回类型是什么。但是具体是不是存在，函数声明决定不了。
2. 函数的声明一般出现在函数的使用之前。要满足先声明后使用。
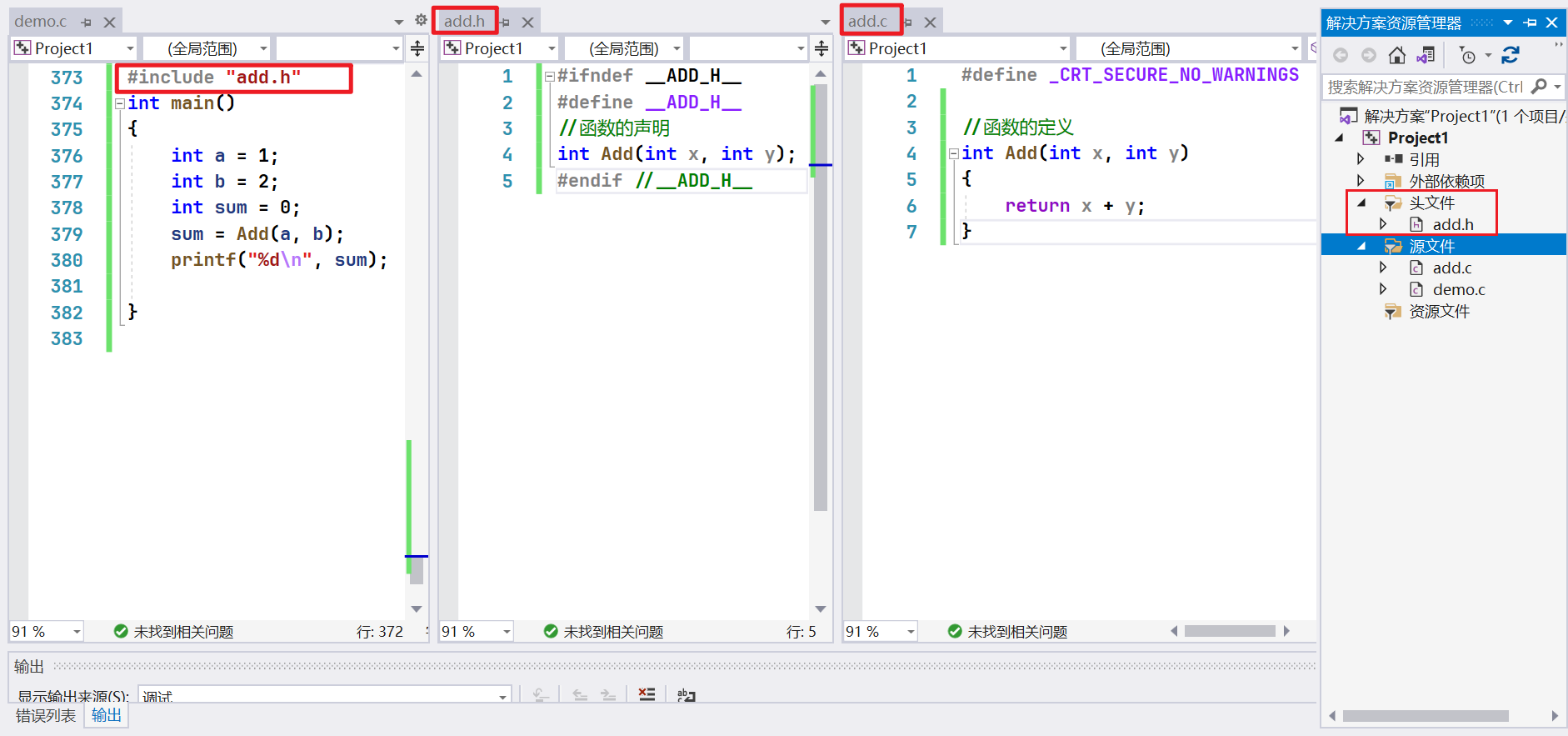
3. 函数的声明一般要放在头文件中的。

5.2 函数的定义

函数的定义是指函数的具体实现，交待函数的功能实现。

注意：
函数的声明放在头文件中，定义放在单独的.c 文件中。

自己创建的函数需要引头文件，#include "add.h" 。
#ifndef __ADD_H__ #define __ADD_H__ #define __ADD_H__ 是为了防止同一个头文件被引用多次。

6 函数的递归

6.1 什么是递归

程序调用自身的编程技巧称为递归（ recursion）

简单的递归：

int main()
{
	printf("hehe")
	main()
	return 0;
}

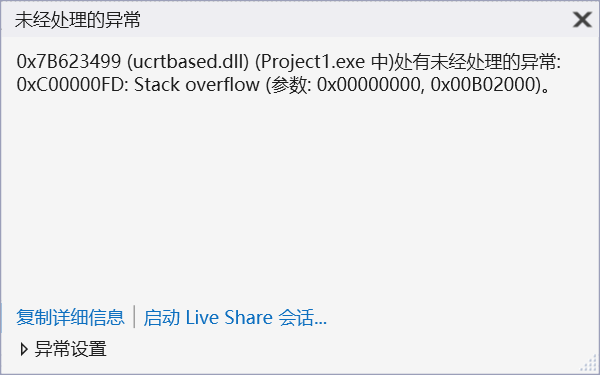
会报错：Stack overflow 栈溢出

6.2 递归的两个必要条件

• 存在限制条件，当满足这个限制条件的时候，递归便不再继续。
• 每次递归调用之后越来越接近这个限制条件。

6.3 练习

练习1

// 接受一个整型值（无符号），按照顺序打印它的每一位。
void print_num(int n)
{
	if (n > 9) 
	{
		print_num(n / 10);
	}
		printf("%d ", n % 10);
}

int main()
{
	unsigned int num = 0;
	scanf("%d", &num);
	print_num(num);
	return 0;
}

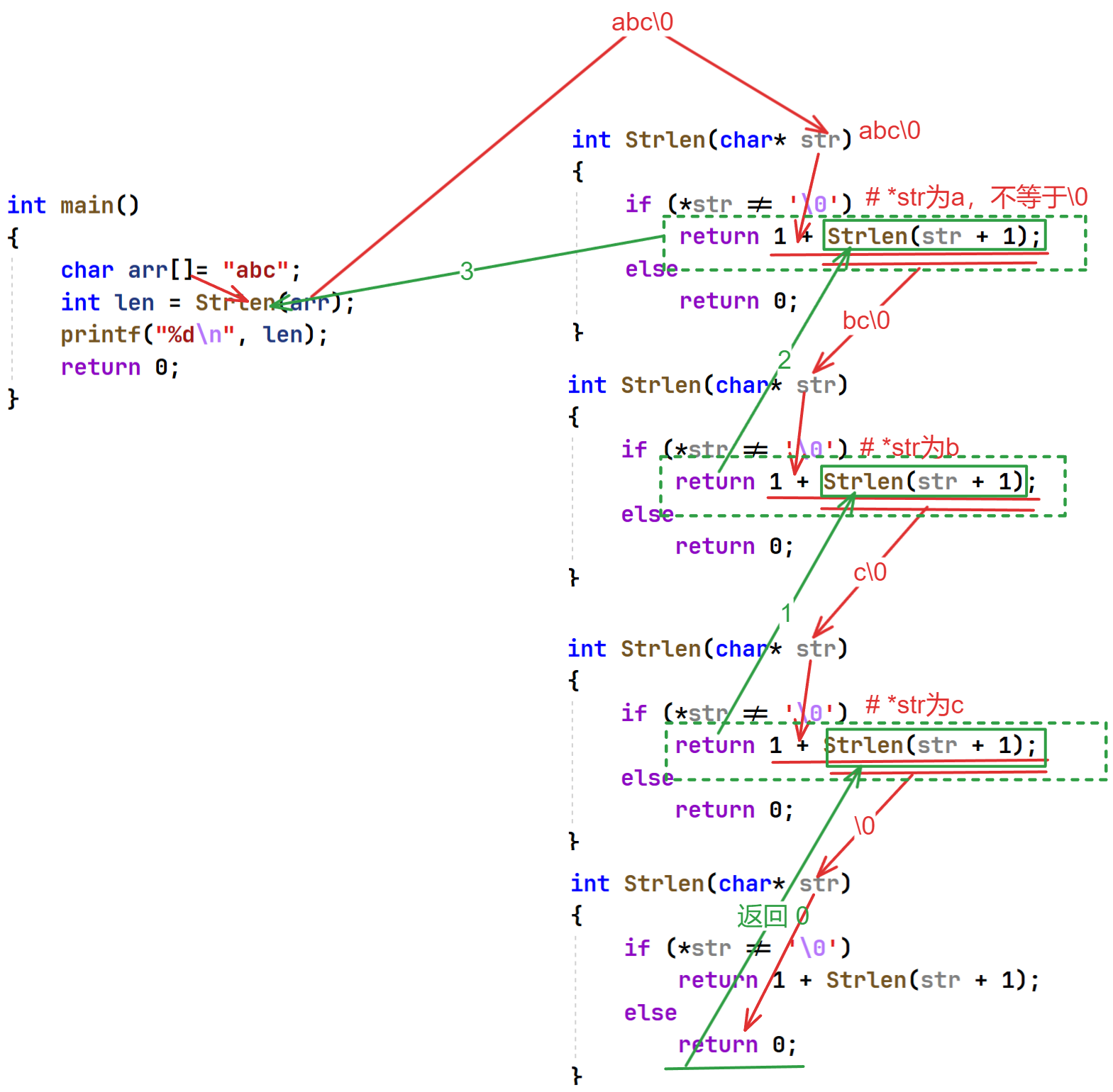
练习2

//编写函数不允许创建临时变量，求字符串的长度。
#include <stdio.h>
int Strlen(const char* str)
{
	if (*str == '\0')
		return 0;
	else
		return 1 + Strlen(str + 1);
}
int main()
{
	char* p = "abcdef";
	int len = Strlen(p);
	printf("%d\n", len);
	return 0;
}

6.4 递归与迭代

6.4.1 练习3

// 求n的阶乘
int Fac(int n)
{
	if (n <= 1) 
		return 1;
	else
		return n * Fac(n - 1);
}

int main()
{
	int num = 0;
	int ret = 0;
	scanf("%d", &num);

	ret = Fac(num);
	printf("%d", ret);
	
}

6.4.2 练习4

//求第n个斐波那契数。（不考虑溢出）
int fib(int n)
{
	if (n <= 2)
		return 1;
	else
		return fib(n - 1) + fib(n - 2);
}

但是：

• 使用fib这个函数计算第50个斐波那契数字的时候特别耗费时间。
• 使用Fac 函数求10000的阶乘，程序会崩溃。

为什么呢？
其实fib函数在调用的时候在一直重复计算。
我们来看一下计算了多少次，修改代码如下：

int count = 0;
int Fac(int n)
{
	if (n = 3)
		count++;
	if (n <= 1) 
		return 1;
	else
		return n * Fac(n - 1);
}

结果中的count非常非常大。在调试Fac函数的时候，如果参数比较大，那就会报错： stack overflow（栈溢出）
因为，系统分配给程序的栈空间是有限的，如果出现了死循环，或者死递），这样有可能导致一直开辟栈空间，最终耗尽栈空间，这样的现象我们称为栈溢出。

如何解决这种情况？

1. 将递归改写成非递归。
2. 使用static 对象替代nonstatic 局部对象（即栈对象）。这不仅可以减少每次递归调用和返回时产生和释放nonstatic 对象的开销，而且static 对象还可以保存递归调用的中间状态，并且可为各个调用层所访问。

采用非递归的方法计算斐波那契数（P41 33:00）：

int Fac(int n)
{
	int a = 1;
	int b = 1;
	int c = 1;

	while (n>2)
	{
		c = a + b;
		a = b;
		b = c;
		n--;
	}
	return c;
}

1. 许多问题是以递归的形式进行解释的，这只是因为它比非递归的形式更为清晰。
2. 但是这些问题的迭代实现往往比递归实现效率更高，虽然代码的可读性稍微差些。
3. 当一个问题相当复杂，难以用迭代实现时，此时递归实现的简洁性便可以补偿它所带来的运行时开销。