工业蒸汽预测-02数据探索
1导入数据探索的工具包
1 | |
2读取数据
使用Pandas库read_csv()函数进行数据读取,由于读取的是文本文件(.txt),需要设置分割符为‘\t’
1 | |
3查看数据信息
3.1查看数据基本信息
1 | |
<class 'pandas.core.frame.DataFrame'>
RangeIndex: 2888 entries, 0 to 2887
Data columns (total 39 columns):
# Column Non-Null Count Dtype
--- ------ -------------- -----
0 V0 2888 non-null float64
1 V1 2888 non-null float64
2 V2 2888 non-null float64
3 V3 2888 non-null float64
4 V4 2888 non-null float64
5 V5 2888 non-null float64
6 V6 2888 non-null float64
7 V7 2888 non-null float64
8 V8 2888 non-null float64
9 V9 2888 non-null float64
10 V10 2888 non-null float64
11 V11 2888 non-null float64
12 V12 2888 non-null float64
13 V13 2888 non-null float64
14 V14 2888 non-null float64
15 V15 2888 non-null float64
16 V16 2888 non-null float64
17 V17 2888 non-null float64
18 V18 2888 non-null float64
19 V19 2888 non-null float64
20 V20 2888 non-null float64
21 V21 2888 non-null float64
22 V22 2888 non-null float64
23 V23 2888 non-null float64
24 V24 2888 non-null float64
25 V25 2888 non-null float64
26 V26 2888 non-null float64
27 V27 2888 non-null float64
28 V28 2888 non-null float64
29 V29 2888 non-null float64
30 V30 2888 non-null float64
31 V31 2888 non-null float64
32 V32 2888 non-null float64
33 V33 2888 non-null float64
34 V34 2888 non-null float64
35 V35 2888 non-null float64
36 V36 2888 non-null float64
37 V37 2888 non-null float64
38 target 2888 non-null float64
dtypes: float64(39)
memory usage: 880.1 KB
- 此训练集数据共有2888个样本,数据中有V0-V37共计38个特征变量,变量类型都为数值类型,所有数据特征没有缺失值数据;
- 数据字段由于采用了脱敏处理,删除了特征数据的具体含义;
- target字段为标签变量
1 | |
<class 'pandas.core.frame.DataFrame'>
RangeIndex: 1925 entries, 0 to 1924
Data columns (total 38 columns):
# Column Non-Null Count Dtype
--- ------ -------------- -----
0 V0 1925 non-null float64
1 V1 1925 non-null float64
2 V2 1925 non-null float64
3 V3 1925 non-null float64
4 V4 1925 non-null float64
5 V5 1925 non-null float64
6 V6 1925 non-null float64
7 V7 1925 non-null float64
8 V8 1925 non-null float64
9 V9 1925 non-null float64
10 V10 1925 non-null float64
11 V11 1925 non-null float64
12 V12 1925 non-null float64
13 V13 1925 non-null float64
14 V14 1925 non-null float64
15 V15 1925 non-null float64
16 V16 1925 non-null float64
17 V17 1925 non-null float64
18 V18 1925 non-null float64
19 V19 1925 non-null float64
20 V20 1925 non-null float64
21 V21 1925 non-null float64
22 V22 1925 non-null float64
23 V23 1925 non-null float64
24 V24 1925 non-null float64
25 V25 1925 non-null float64
26 V26 1925 non-null float64
27 V27 1925 non-null float64
28 V28 1925 non-null float64
29 V29 1925 non-null float64
30 V30 1925 non-null float64
31 V31 1925 non-null float64
32 V32 1925 non-null float64
33 V33 1925 non-null float64
34 V34 1925 non-null float64
35 V35 1925 non-null float64
36 V36 1925 non-null float64
37 V37 1925 non-null float64
dtypes: float64(38)
memory usage: 571.6 KB
- 测试集数据共有1925个样本,数据中有V0-V37共计38个特征变量,变量类型都为数值类型,无缺失值。
- 测试集中没有target字段(标签变量),需要我们预测并提交。
3.2查看数据统计信息
1 | |
| V0 | V1 | V2 | V3 | V4 | V5 | V6 | V7 | V8 | V9 | ... | V29 | V30 | V31 | V32 | V33 | V34 | V35 | V36 | V37 | target | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| count | 2888.000000 | 2888.000000 | 2888.000000 | 2888.000000 | 2888.000000 | 2888.000000 | 2888.000000 | 2888.000000 | 2888.000000 | 2888.000000 | ... | 2888.000000 | 2888.000000 | 2888.000000 | 2888.000000 | 2888.000000 | 2888.000000 | 2888.000000 | 2888.000000 | 2888.000000 | 2888.000000 |
| mean | 0.123048 | 0.056068 | 0.289720 | -0.067790 | 0.012921 | -0.558565 | 0.182892 | 0.116155 | 0.177856 | -0.169452 | ... | 0.097648 | 0.055477 | 0.127791 | 0.020806 | 0.007801 | 0.006715 | 0.197764 | 0.030658 | -0.130330 | 0.126353 |
| std | 0.928031 | 0.941515 | 0.911236 | 0.970298 | 0.888377 | 0.517957 | 0.918054 | 0.955116 | 0.895444 | 0.953813 | ... | 1.061200 | 0.901934 | 0.873028 | 0.902584 | 1.006995 | 1.003291 | 0.985675 | 0.970812 | 1.017196 | 0.983966 |
| min | -4.335000 | -5.122000 | -3.420000 | -3.956000 | -4.742000 | -2.182000 | -4.576000 | -5.048000 | -4.692000 | -12.891000 | ... | -2.912000 | -4.507000 | -5.859000 | -4.053000 | -4.627000 | -4.789000 | -5.695000 | -2.608000 | -3.630000 | -3.044000 |
| 25% | -0.297000 | -0.226250 | -0.313000 | -0.652250 | -0.385000 | -0.853000 | -0.310000 | -0.295000 | -0.159000 | -0.390000 | ... | -0.664000 | -0.283000 | -0.170250 | -0.407250 | -0.499000 | -0.290000 | -0.202500 | -0.413000 | -0.798250 | -0.350250 |
| 50% | 0.359000 | 0.272500 | 0.386000 | -0.044500 | 0.110000 | -0.466000 | 0.388000 | 0.344000 | 0.362000 | 0.042000 | ... | -0.023000 | 0.053500 | 0.299500 | 0.039000 | -0.040000 | 0.160000 | 0.364000 | 0.137000 | -0.185500 | 0.313000 |
| 75% | 0.726000 | 0.599000 | 0.918250 | 0.624000 | 0.550250 | -0.154000 | 0.831250 | 0.782250 | 0.726000 | 0.042000 | ... | 0.745250 | 0.488000 | 0.635000 | 0.557000 | 0.462000 | 0.273000 | 0.602000 | 0.644250 | 0.495250 | 0.793250 |
| max | 2.121000 | 1.918000 | 2.828000 | 2.457000 | 2.689000 | 0.489000 | 1.895000 | 1.918000 | 2.245000 | 1.335000 | ... | 4.580000 | 2.689000 | 2.013000 | 2.395000 | 5.465000 | 5.110000 | 2.324000 | 5.238000 | 3.000000 | 2.538000 |
8 rows × 39 columns
上面数据显示了数据的统计信息,例如样本数count,数据的平均值mean,标准差std,最小值min,最大值max等
1 | |
| V0 | V1 | V2 | V3 | V4 | V5 | V6 | V7 | V8 | V9 | ... | V28 | V29 | V30 | V31 | V32 | V33 | V34 | V35 | V36 | V37 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| count | 1925.000000 | 1925.000000 | 1925.000000 | 1925.000000 | 1925.000000 | 1925.000000 | 1925.000000 | 1925.000000 | 1925.000000 | 1925.000000 | ... | 1925.000000 | 1925.000000 | 1925.000000 | 1925.000000 | 1925.000000 | 1925.000000 | 1925.000000 | 1925.000000 | 1925.000000 | 1925.000000 |
| mean | -0.184404 | -0.083912 | -0.434762 | 0.101671 | -0.019172 | 0.838049 | -0.274092 | -0.173971 | -0.266709 | 0.255114 | ... | -0.206871 | -0.146463 | -0.083215 | -0.191729 | -0.030782 | -0.011433 | -0.009985 | -0.296895 | -0.046270 | 0.195735 |
| std | 1.073333 | 1.076670 | 0.969541 | 1.034925 | 1.147286 | 0.963043 | 1.054119 | 1.040101 | 1.085916 | 1.014394 | ... | 1.064140 | 0.880593 | 1.126414 | 1.138454 | 1.130228 | 0.989732 | 0.995213 | 0.946896 | 1.040854 | 0.940599 |
| min | -4.814000 | -5.488000 | -4.283000 | -3.276000 | -4.921000 | -1.168000 | -5.649000 | -5.625000 | -6.059000 | -6.784000 | ... | -2.435000 | -2.413000 | -4.507000 | -7.698000 | -4.057000 | -4.627000 | -4.789000 | -7.477000 | -2.608000 | -3.346000 |
| 25% | -0.664000 | -0.451000 | -0.978000 | -0.644000 | -0.497000 | 0.122000 | -0.732000 | -0.509000 | -0.775000 | -0.390000 | ... | -0.453000 | -0.818000 | -0.339000 | -0.476000 | -0.472000 | -0.460000 | -0.290000 | -0.349000 | -0.593000 | -0.432000 |
| 50% | 0.065000 | 0.195000 | -0.267000 | 0.220000 | 0.118000 | 0.437000 | -0.082000 | 0.018000 | -0.004000 | 0.401000 | ... | -0.445000 | -0.199000 | 0.010000 | 0.100000 | 0.155000 | -0.040000 | 0.160000 | -0.270000 | 0.083000 | 0.152000 |
| 75% | 0.549000 | 0.589000 | 0.278000 | 0.793000 | 0.610000 | 1.928000 | 0.457000 | 0.515000 | 0.482000 | 0.904000 | ... | -0.434000 | 0.468000 | 0.447000 | 0.471000 | 0.627000 | 0.419000 | 0.273000 | 0.364000 | 0.651000 | 0.797000 |
| max | 2.100000 | 2.120000 | 1.946000 | 2.603000 | 4.475000 | 3.176000 | 1.528000 | 1.394000 | 2.408000 | 1.766000 | ... | 4.656000 | 3.022000 | 3.139000 | 1.428000 | 2.299000 | 5.465000 | 5.110000 | 1.671000 | 2.861000 | 3.021000 |
8 rows × 38 columns
3.3查看数据字段信息
1 | |
| V0 | V1 | V2 | V3 | V4 | V5 | V6 | V7 | V8 | V9 | ... | V29 | V30 | V31 | V32 | V33 | V34 | V35 | V36 | V37 | target | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0.566 | 0.016 | -0.143 | 0.407 | 0.452 | -0.901 | -1.812 | -2.360 | -0.436 | -2.114 | ... | 0.136 | 0.109 | -0.615 | 0.327 | -4.627 | -4.789 | -5.101 | -2.608 | -3.508 | 0.175 |
| 1 | 0.968 | 0.437 | 0.066 | 0.566 | 0.194 | -0.893 | -1.566 | -2.360 | 0.332 | -2.114 | ... | -0.128 | 0.124 | 0.032 | 0.600 | -0.843 | 0.160 | 0.364 | -0.335 | -0.730 | 0.676 |
| 2 | 1.013 | 0.568 | 0.235 | 0.370 | 0.112 | -0.797 | -1.367 | -2.360 | 0.396 | -2.114 | ... | -0.009 | 0.361 | 0.277 | -0.116 | -0.843 | 0.160 | 0.364 | 0.765 | -0.589 | 0.633 |
| 3 | 0.733 | 0.368 | 0.283 | 0.165 | 0.599 | -0.679 | -1.200 | -2.086 | 0.403 | -2.114 | ... | 0.015 | 0.417 | 0.279 | 0.603 | -0.843 | -0.065 | 0.364 | 0.333 | -0.112 | 0.206 |
| 4 | 0.684 | 0.638 | 0.260 | 0.209 | 0.337 | -0.454 | -1.073 | -2.086 | 0.314 | -2.114 | ... | 0.183 | 1.078 | 0.328 | 0.418 | -0.843 | -0.215 | 0.364 | -0.280 | -0.028 | 0.384 |
5 rows × 39 columns
上面显示训练集前5条数据的基本信息,可以看到数据都是浮点型数据,数据都是数值型连续型特征
1 | |
| V0 | V1 | V2 | V3 | V4 | V5 | V6 | V7 | V8 | V9 | ... | V28 | V29 | V30 | V31 | V32 | V33 | V34 | V35 | V36 | V37 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0.368 | 0.380 | -0.225 | -0.049 | 0.379 | 0.092 | 0.550 | 0.551 | 0.244 | 0.904 | ... | -0.449 | 0.047 | 0.057 | -0.042 | 0.847 | 0.534 | -0.009 | -0.190 | -0.567 | 0.388 |
| 1 | 0.148 | 0.489 | -0.247 | -0.049 | 0.122 | -0.201 | 0.487 | 0.493 | -0.127 | 0.904 | ... | -0.443 | 0.047 | 0.560 | 0.176 | 0.551 | 0.046 | -0.220 | 0.008 | -0.294 | 0.104 |
| 2 | -0.166 | -0.062 | -0.311 | 0.046 | -0.055 | 0.063 | 0.485 | 0.493 | -0.227 | 0.904 | ... | -0.458 | -0.398 | 0.101 | 0.199 | 0.634 | 0.017 | -0.234 | 0.008 | 0.373 | 0.569 |
| 3 | 0.102 | 0.294 | -0.259 | 0.051 | -0.183 | 0.148 | 0.474 | 0.504 | 0.010 | 0.904 | ... | -0.456 | -0.398 | 1.007 | 0.137 | 1.042 | -0.040 | -0.290 | 0.008 | -0.666 | 0.391 |
| 4 | 0.300 | 0.428 | 0.208 | 0.051 | -0.033 | 0.116 | 0.408 | 0.497 | 0.155 | 0.904 | ... | -0.458 | -0.776 | 0.291 | 0.370 | 0.181 | -0.040 | -0.290 | 0.008 | -0.140 | -0.497 |
5 rows × 38 columns
4可视化数据分布
4.1箱形图
1 | |
<AxesSubplot:>
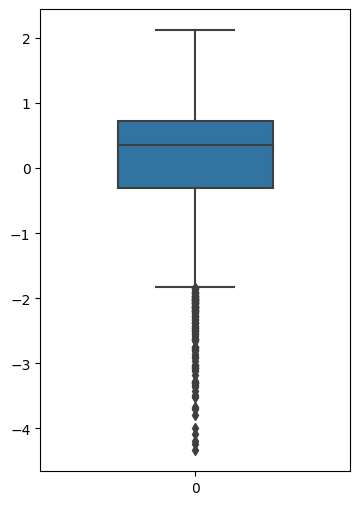
从图中可以看出有偏离值,许多数据点位于下四分位点以下。
代码详解:
fig = plt.figure(figsize=(4, 6))创建一个画布,并指定宽度为4,高度为6。plt是 matplotlib 库的一个模块,用于绘制数据可视化图形。sns.boxplot(train_data['V0'],orient="v", width=0.5)绘制箱形图。sns是 seaborn 库的一个模块,用于数据可视化。boxplot是用于绘制箱形图的函数。train_data['V0']表示从训练集中获取特征变量 V0 的数据进行绘制。orient="v"表示将箱形图垂直绘制,即以竖直方向为主轴。width=0.5表示箱形图的宽度为0.5。
箱形图是一种用于展示数据分布和离群值的图形。它由一个矩形框和两条线(即“须”上限、下限)组成。矩形框表示数据的四分位数范围(上下四分位数之间的距离),中间的线表示中位数,须表示数据的整体分布情况。箱形图可以帮助我们观察数据的偏态、集中趋势以及离群值等信息
1 | |
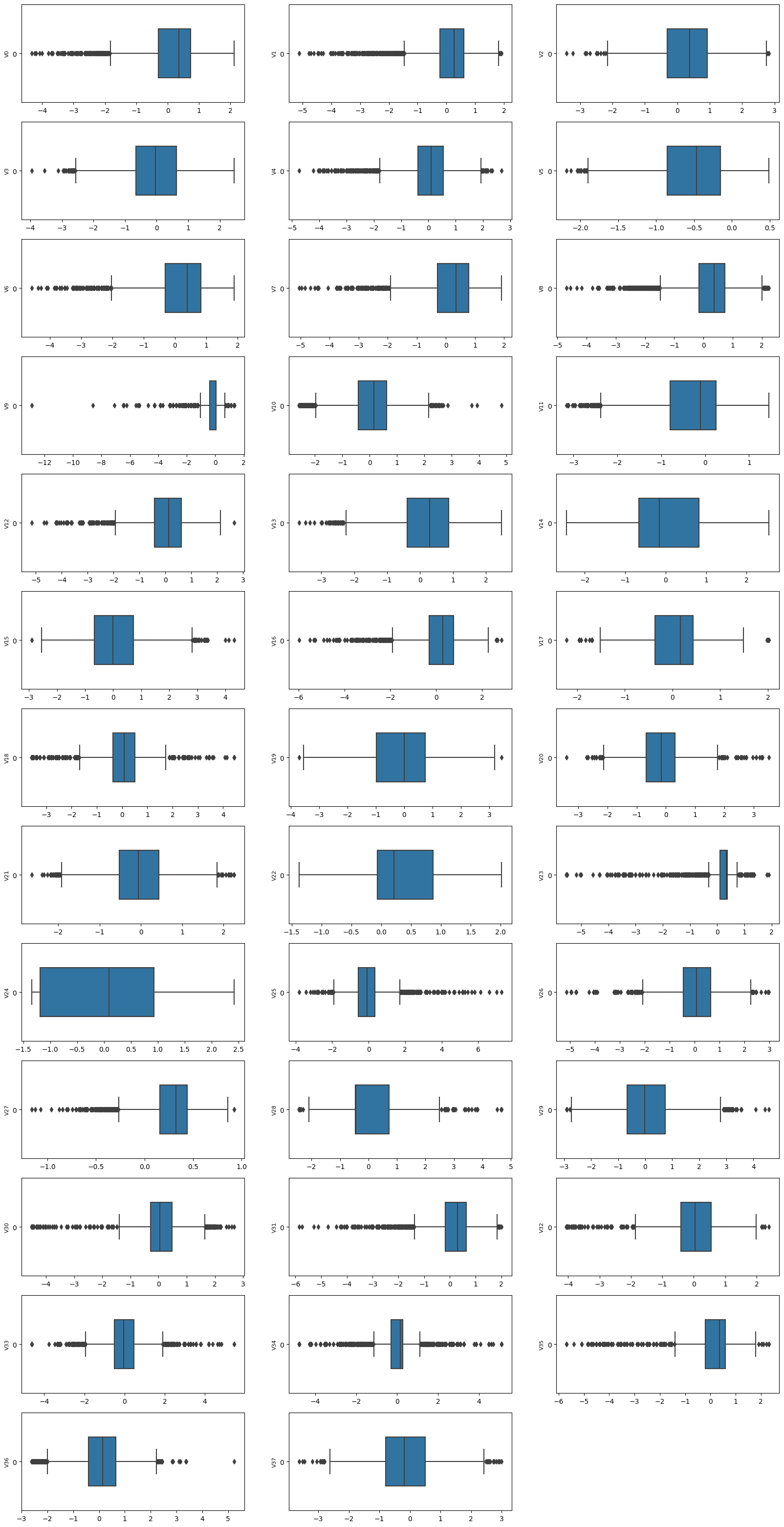
从图中发现数据存在许多偏离较大的异常值,可以考虑移除。
代码详解:
column = train_data.columns.tolist()[:39]获取训练集数据中前39(包含)列(即V0到target)的列名,并将其存储在列表column中。train_data.columns返回数据集的所有列名,tolist()将其转换为列表,[:39]表示取列表中的前39个元素。fig = plt.figure(figsize=(20, 40))创建一个画布,并指定宽度为20,高度为40。for i in range(38):循环遍历从0到37的整数,对应特征变量 V0 到 V37。plt.subplot(13, 3, i + 1)创建一个子图,将画布分为13行3列的网格,选中当前子图(i+1)进行绘制。i + 1表示子图的编号,从1开始。sns.boxplot(train_data[column[i]], orient="h", width=0.5)绘制箱形图。train_data[column[i]]表示从训练集中获取第i个特征变量的数据进行绘制。orient="h"表示将箱形图水平绘制,即以水平方向为主轴。width=0.5表示箱形图的宽度为0.5。plt.ylabel(column[i], fontsize=8)在每个子图上添加y轴标签,标签内容为对应的特征变量名称column[i],并设置字体大小为8。plt.show()展示绘制的箱形图。
4.2直方图和Q-Q图
Q-Q图是指数据的分位数和正态分布的分位数对比参照的图,如果数据符合正态分布,则所有的点都会落在直线上。
1 | |
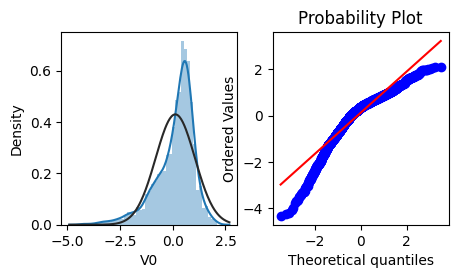
可以看到,训练集中特征变量V0的分布不是正态分布。
代码详解:
plt.figure(figsize=(10,5))创建一个宽度为10,高度为5的画布对象。figsize=(10,5)指定了画布的尺寸。ax=plt.subplot(1,2,1)创建一个子图对象,并指定它位于画布的第1行,第2列中。这里的(1,2,1)表示将画布分为1行2列的网格,并选中第1个位置的子图。sns.distplot(train_data['V0'],fit=stats.norm)在第一个子图中绘制特征变量 ‘V0’ 的直方图。train_data['V0']表示从训练集中获取 ‘V0’ 特征变量的数据进行绘制。sns.distplot()是 seaborn 库中的函数,用于绘制直方图并拟合参数化的概率密度函数(默认为正态分布,通过fit=stats.norm指定,表示使用正态分布拟合)。ax=plt.subplot(1,2,2)创建第二个子图,并指定它位于画布的第1行,第2列中。这里的(1,2,2)表示将画布分为1行2列的网格,并选中第2个位置的子图。res = stats.probplot(train_data['V0'], plot=plt)在第二个子图中绘制特征变量 ‘V0’ 的概率图。stats.probplot()是 scipy 库(科学计算库)中的函数,用于绘制概率图。它可以判断数据是否符合某种理论分布(这里使用了默认的正态分布)。plot=plt表示将概率图绘制在指定的子图上。
1 | |
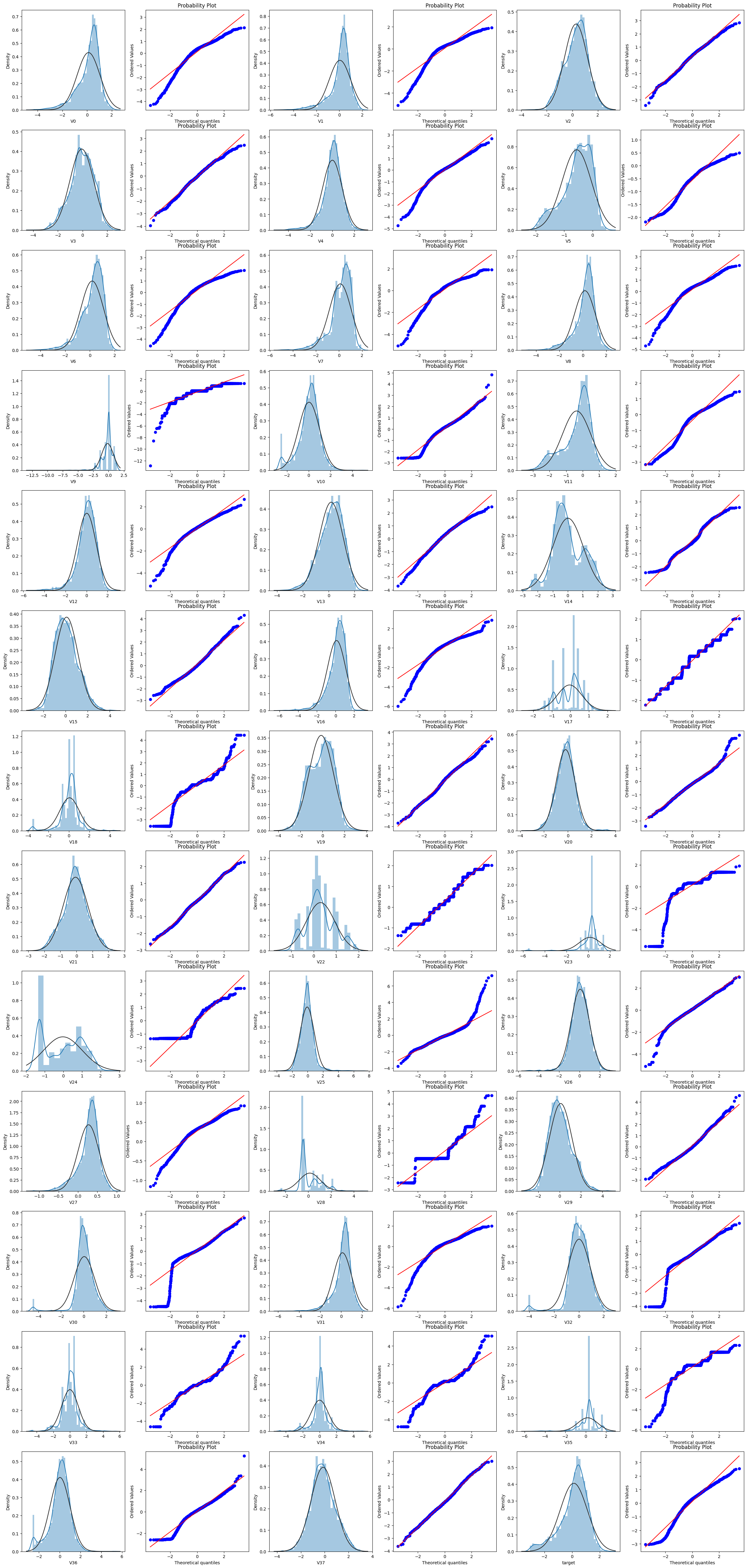
由上面的数据分布图信息可以看出,很多特征变量(如’V1’,’V9’,’V24’,’V28’等)的数据分布不是正态的,数据并不跟随对角线,后续可以使用数据变换对数据进行转换。
代码解释:
简单的图可以通过plt.figure(figsize=(10, 5))直接指定画布的大小。
在展示多个子图时,直接指定画布大小可能会导致子图之间的重叠或缺乏足够的空间来显示所有子图。从而导致布局混乱或信息重叠。
使用plt.figure(figsize=(5*train_cols, 5*train_rows))的方式更加灵活,它会自动根据数据集中的特征变量数量来计算所需的行数和列数,并相应地调整画布的大小。这样可以确保每个子图都有足够的空间进行展示,并且整体布局更加均衡和清晰。
4.3KDE图
KDE(Kernel Density Estimation,核密度估计)可以理解为是对直方图的加窗平滑。可以查看并对比训练集和测试集中特征变量的分布情况,发现两个数据集中分布不一致的特征变量。
1 | |
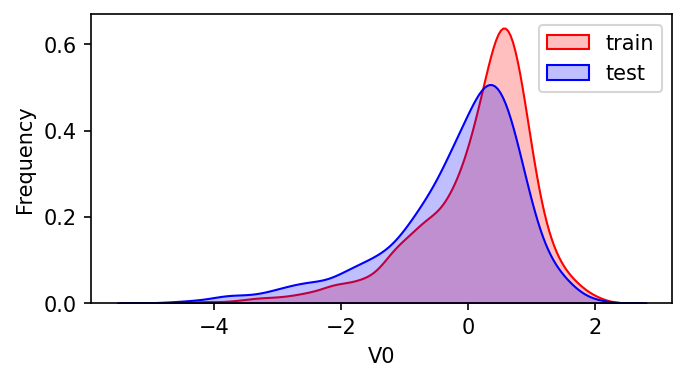
可以看到,V0在两个数据集中的分布基本一致。
代码详解:
plt.figure(figsize=(8,4), dpi=150):创建一个画布,指定尺寸为宽度8英寸,高度4英寸,dpi(每英寸像素点数)为150,数值越高质量越好,不指定有默认。ax = sns.kdeplot(train_data['V0'], color="Red", shade=True):使用 Seaborn 库的kdeplot函数绘制训练数据集中特征变量'V0'的核密度估计曲线。color="Red"指定曲线的颜色为红色,shade=True表示曲线下方填充阴影以突出密度分布。ax = sns.kdeplot(test_data['V0'], color="Blue", shade=True):类似地,使用kdeplot函数在同一图形上绘制测试数据集中特征变量'V0'的核密度估计曲线。这里设置曲线颜色为蓝色。ax.set_xlabel('V0'):设置 x 轴的标签为'V0'。ax.set_ylabel("Frequency"):设置 y 轴的标签为'Frequency'。ax = ax.legend(["train","test"]):添加图例。该语句首先通过ax.legend()方法在当前的轴对象ax上添加图例,然后使用["train", "test"]指定图例的标签。
1 | |
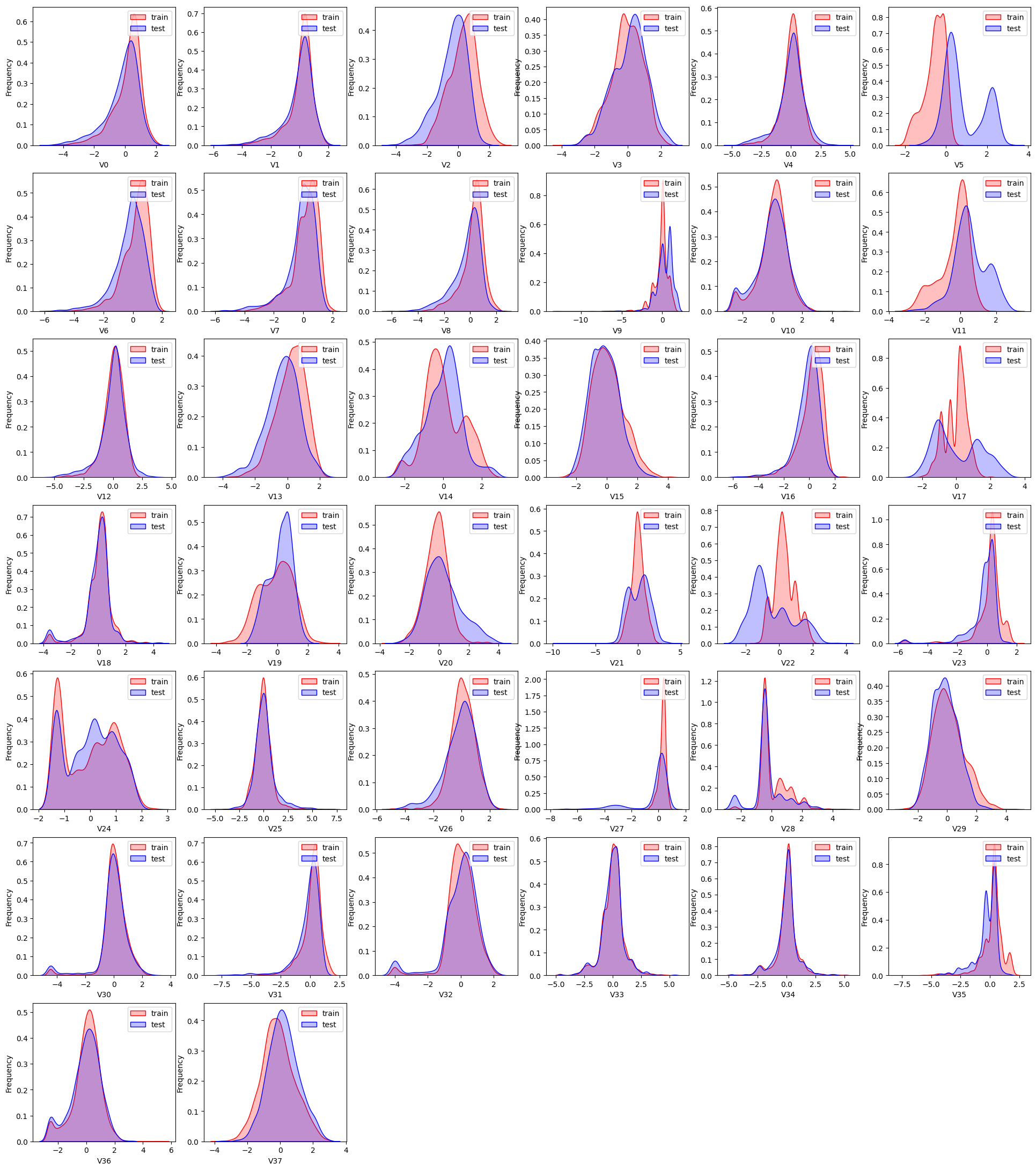
可以发现,特征变量V5,V9,V11,V17,V22,V28在训练集与测试集中的分布不一致
1 | |

由上图的数据分布可以看到特征’V5’,’V9’,’V11’,’V17’,’V22’,’V28’ 训练集数据与测试集数据分布不一致,会导致模型泛化能力差,采用删除此类特征方法。
1 | |
1 | |
4.4线性回归关系图
线性回归关系图主要用于分析变量之间的线性回归关系。
1 | |
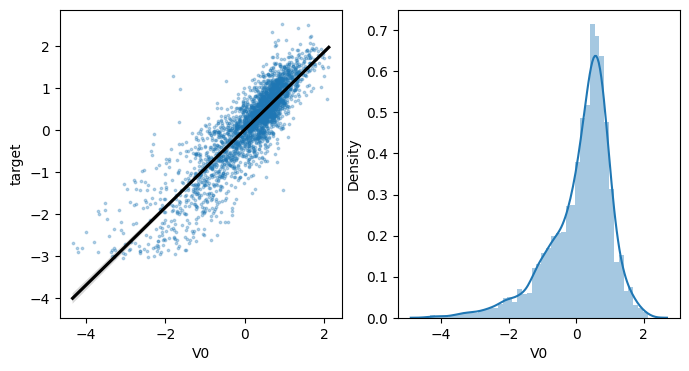
1 | |
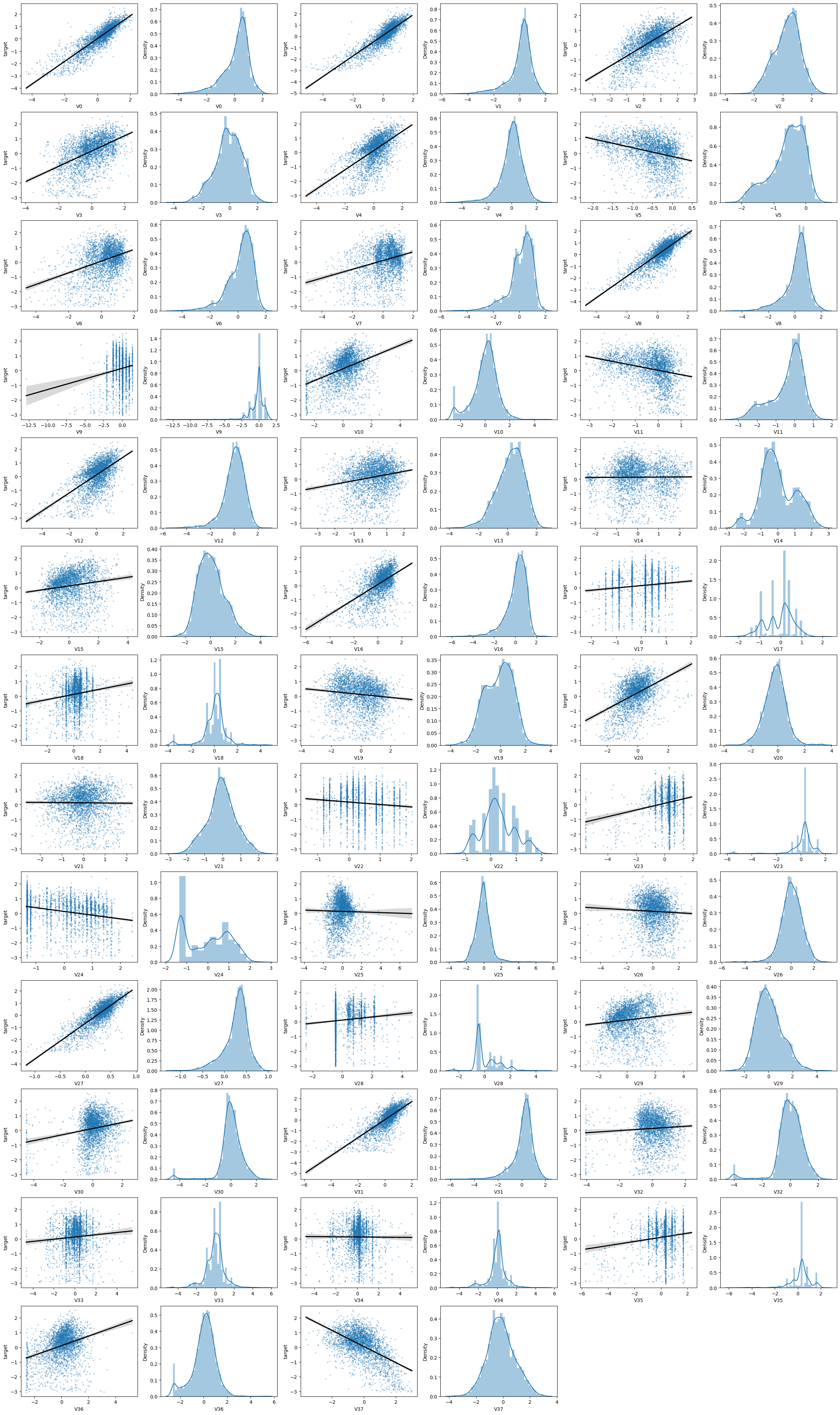
代码解释:
散点图:
使用 Seaborn 库中的 regplot 函数来绘制自变量 col 与因变量 'target' 之间的散点图,并拟合一条线性回归线。
x=col表示自变量的数据是col,即当前循环遍历到的特征变量。y='target'表示因变量的数据是'target',即目标变量。data=train_data表示数据集是train_data,即训练数据集。ax=ax表示将子图对象ax分配给regplot函数来绘制子图。scatter_kws={'marker':'.','s':3,'alpha':0.3}设置散点图的样式参数。这里使用了小圆点作为散点图的标记,设置了透明度(alpha)、大小(s)和颜色(默认颜色)。line_kws={'color':'k'}设置回归线的样式参数。这里将回归线的颜色设置为黑色('k'是黑色的简写)。
直方图:sns.distplot(train_data[col].dropna()) 绘制特征变量 col 的直方图和核密度估计曲线。dropna()函数用于移除其中的缺失值(NaN值)。
5查看特征变量的相关性
对特征变量的相关性进行分析,可以发现特征变量和目标变量及特征变量之间的关系,为在特征工程中提取特征做准备。
5.1计算相关性系数
在删除训练集和测试集中分布不一致的特征变量,如V5,V9,V11,V17,V22,V28之后,计算剩余特征变量及taret变量的相关性系数。
1 | |
| V0 | V1 | V2 | V3 | V4 | V6 | V7 | V8 | V10 | V12 | ... | V29 | V30 | V31 | V32 | V33 | V34 | V35 | V36 | V37 | target | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| V0 | 1.000000 | 0.908607 | 0.463643 | 0.409576 | 0.781212 | 0.189267 | 0.141294 | 0.794013 | 0.298443 | 0.751830 | ... | 0.302145 | 0.156968 | 0.675003 | 0.050951 | 0.056439 | -0.019342 | 0.138933 | 0.231417 | -0.494076 | 0.873212 |
| V1 | 0.908607 | 1.000000 | 0.506514 | 0.383924 | 0.657790 | 0.276805 | 0.205023 | 0.874650 | 0.310120 | 0.656186 | ... | 0.147096 | 0.175997 | 0.769745 | 0.085604 | 0.035129 | -0.029115 | 0.146329 | 0.235299 | -0.494043 | 0.871846 |
| V2 | 0.463643 | 0.506514 | 1.000000 | 0.410148 | 0.057697 | 0.615938 | 0.477114 | 0.703431 | 0.346006 | 0.059941 | ... | -0.275764 | 0.175943 | 0.653764 | 0.033942 | 0.050309 | -0.025620 | 0.043648 | 0.316462 | -0.734956 | 0.638878 |
| V3 | 0.409576 | 0.383924 | 0.410148 | 1.000000 | 0.315046 | 0.233896 | 0.197836 | 0.411946 | 0.321262 | 0.306397 | ... | 0.117610 | 0.043966 | 0.421954 | -0.092423 | -0.007159 | -0.031898 | 0.080034 | 0.324475 | -0.229613 | 0.512074 |
| V4 | 0.781212 | 0.657790 | 0.057697 | 0.315046 | 1.000000 | -0.117529 | -0.052370 | 0.449542 | 0.141129 | 0.927685 | ... | 0.659093 | 0.022807 | 0.447016 | -0.026186 | 0.062367 | 0.028659 | 0.100010 | 0.113609 | -0.031054 | 0.603984 |
| V6 | 0.189267 | 0.276805 | 0.615938 | 0.233896 | -0.117529 | 1.000000 | 0.917502 | 0.468233 | 0.415660 | -0.087312 | ... | -0.467980 | 0.188907 | 0.546535 | 0.144550 | 0.054210 | -0.002914 | 0.044992 | 0.433804 | -0.404817 | 0.370037 |
| V7 | 0.141294 | 0.205023 | 0.477114 | 0.197836 | -0.052370 | 0.917502 | 1.000000 | 0.389987 | 0.310982 | -0.036791 | ... | -0.311363 | 0.170113 | 0.475254 | 0.122707 | 0.034508 | -0.019103 | 0.111166 | 0.340479 | -0.292285 | 0.287815 |
| V8 | 0.794013 | 0.874650 | 0.703431 | 0.411946 | 0.449542 | 0.468233 | 0.389987 | 1.000000 | 0.419703 | 0.420557 | ... | -0.011091 | 0.150258 | 0.878072 | 0.038430 | 0.026843 | -0.036297 | 0.179167 | 0.326586 | -0.553121 | 0.831904 |
| V10 | 0.298443 | 0.310120 | 0.346006 | 0.321262 | 0.141129 | 0.415660 | 0.310982 | 0.419703 | 1.000000 | 0.140462 | ... | -0.105042 | -0.036705 | 0.560213 | -0.093213 | 0.016739 | -0.026994 | 0.026846 | 0.922190 | -0.045851 | 0.394767 |
| V12 | 0.751830 | 0.656186 | 0.059941 | 0.306397 | 0.927685 | -0.087312 | -0.036791 | 0.420557 | 0.140462 | 1.000000 | ... | 0.666775 | 0.028866 | 0.441963 | -0.007658 | 0.046674 | 0.010122 | 0.081963 | 0.112150 | -0.054827 | 0.594189 |
| V13 | 0.185144 | 0.157518 | 0.204762 | -0.003636 | 0.075993 | 0.138367 | 0.110973 | 0.153299 | -0.059553 | 0.098771 | ... | 0.008235 | 0.027328 | 0.113743 | 0.130598 | 0.157513 | 0.116944 | 0.219906 | -0.024751 | -0.379714 | 0.203373 |
| V14 | -0.004144 | -0.006268 | -0.106282 | -0.232677 | 0.023853 | 0.072911 | 0.163931 | 0.008138 | -0.077543 | 0.020069 | ... | 0.056814 | -0.004057 | 0.010989 | 0.106581 | 0.073535 | 0.043218 | 0.233523 | -0.086217 | 0.010553 | 0.008424 |
| V15 | 0.314520 | 0.164702 | -0.224573 | 0.143457 | 0.615704 | -0.431542 | -0.291272 | 0.018366 | -0.046737 | 0.642081 | ... | 0.951314 | -0.111311 | 0.011768 | -0.104618 | 0.050254 | 0.048602 | 0.100817 | -0.051861 | 0.245635 | 0.154020 |
| V16 | 0.347357 | 0.435606 | 0.782474 | 0.394517 | 0.023818 | 0.847119 | 0.752683 | 0.680031 | 0.546975 | 0.025736 | ... | -0.342210 | 0.154794 | 0.778538 | 0.041474 | 0.028878 | -0.054775 | 0.082293 | 0.551880 | -0.420053 | 0.536748 |
| V18 | 0.148622 | 0.123862 | 0.132105 | 0.022868 | 0.136022 | 0.110570 | 0.098691 | 0.093682 | -0.024693 | 0.119833 | ... | 0.053958 | 0.470341 | 0.079718 | 0.411967 | 0.512139 | 0.365410 | 0.152088 | 0.019603 | -0.181937 | 0.170721 |
| V19 | -0.100294 | -0.092673 | -0.161802 | -0.246008 | -0.205729 | 0.215290 | 0.158371 | -0.144693 | 0.074903 | -0.148319 | ... | -0.205409 | 0.100133 | -0.131542 | 0.144018 | -0.021517 | -0.079753 | -0.220737 | 0.087605 | 0.012115 | -0.114976 |
| V20 | 0.462493 | 0.459795 | 0.298385 | 0.289594 | 0.291309 | 0.136091 | 0.089399 | 0.412868 | 0.207612 | 0.271559 | ... | 0.016233 | 0.086165 | 0.326863 | 0.050699 | 0.009358 | -0.000979 | 0.048981 | 0.161315 | -0.322006 | 0.444965 |
| V21 | -0.029285 | -0.012911 | -0.030932 | 0.114373 | 0.174025 | -0.051806 | -0.065300 | -0.047839 | 0.082288 | 0.144371 | ... | 0.157097 | -0.077945 | 0.053025 | -0.159128 | -0.087561 | -0.053707 | -0.199398 | 0.047340 | 0.315470 | -0.010063 |
| V23 | 0.231136 | 0.222574 | 0.065509 | 0.081374 | 0.196530 | 0.069901 | 0.125180 | 0.174124 | -0.066537 | 0.180049 | ... | 0.116122 | 0.363963 | 0.129783 | 0.367086 | 0.183666 | 0.196681 | 0.635252 | -0.035949 | -0.187582 | 0.226331 |
| V24 | -0.324959 | -0.233556 | 0.010225 | -0.237326 | -0.529866 | 0.072418 | -0.030292 | -0.136898 | -0.029420 | -0.550881 | ... | -0.642370 | 0.033532 | -0.202097 | 0.060608 | -0.134320 | -0.095588 | -0.243738 | -0.041325 | -0.137614 | -0.264815 |
| V25 | -0.200706 | -0.070627 | 0.481785 | -0.100569 | -0.444375 | 0.438610 | 0.316744 | 0.173320 | 0.079805 | -0.448877 | ... | -0.575154 | 0.088238 | 0.201243 | 0.065501 | -0.013312 | -0.030747 | -0.093948 | 0.069302 | -0.246742 | -0.019373 |
| V26 | -0.125140 | -0.043012 | 0.035370 | -0.027685 | -0.080487 | 0.106055 | 0.160566 | 0.015724 | 0.072366 | -0.124111 | ... | -0.133694 | -0.057247 | 0.062879 | -0.004545 | -0.034596 | 0.051294 | 0.085576 | 0.064963 | 0.010880 | -0.046724 |
| V27 | 0.733198 | 0.824198 | 0.726250 | 0.392006 | 0.412083 | 0.474441 | 0.424185 | 0.901100 | 0.246085 | 0.374380 | ... | -0.032772 | 0.208074 | 0.790239 | 0.095127 | 0.030135 | -0.036123 | 0.159884 | 0.226713 | -0.617771 | 0.812585 |
| V29 | 0.302145 | 0.147096 | -0.275764 | 0.117610 | 0.659093 | -0.467980 | -0.311363 | -0.011091 | -0.105042 | 0.666775 | ... | 1.000000 | -0.122817 | -0.004364 | -0.110699 | 0.035272 | 0.035392 | 0.078588 | -0.099309 | 0.285581 | 0.123329 |
| V30 | 0.156968 | 0.175997 | 0.175943 | 0.043966 | 0.022807 | 0.188907 | 0.170113 | 0.150258 | -0.036705 | 0.028866 | ... | -0.122817 | 1.000000 | 0.114318 | 0.695725 | 0.083693 | -0.028573 | -0.027987 | 0.006961 | -0.256814 | 0.187311 |
| V31 | 0.675003 | 0.769745 | 0.653764 | 0.421954 | 0.447016 | 0.546535 | 0.475254 | 0.878072 | 0.560213 | 0.441963 | ... | -0.004364 | 0.114318 | 1.000000 | 0.016782 | 0.016733 | -0.047273 | 0.152314 | 0.510851 | -0.357785 | 0.750297 |
| V32 | 0.050951 | 0.085604 | 0.033942 | -0.092423 | -0.026186 | 0.144550 | 0.122707 | 0.038430 | -0.093213 | -0.007658 | ... | -0.110699 | 0.695725 | 0.016782 | 1.000000 | 0.105255 | 0.069300 | 0.016901 | -0.054411 | -0.162417 | 0.066606 |
| V33 | 0.056439 | 0.035129 | 0.050309 | -0.007159 | 0.062367 | 0.054210 | 0.034508 | 0.026843 | 0.016739 | 0.046674 | ... | 0.035272 | 0.083693 | 0.016733 | 0.105255 | 1.000000 | 0.719126 | 0.167597 | 0.031586 | -0.062715 | 0.077273 |
| V34 | -0.019342 | -0.029115 | -0.025620 | -0.031898 | 0.028659 | -0.002914 | -0.019103 | -0.036297 | -0.026994 | 0.010122 | ... | 0.035392 | -0.028573 | -0.047273 | 0.069300 | 0.719126 | 1.000000 | 0.233616 | -0.019032 | -0.006854 | -0.006034 |
| V35 | 0.138933 | 0.146329 | 0.043648 | 0.080034 | 0.100010 | 0.044992 | 0.111166 | 0.179167 | 0.026846 | 0.081963 | ... | 0.078588 | -0.027987 | 0.152314 | 0.016901 | 0.167597 | 0.233616 | 1.000000 | 0.025401 | -0.077991 | 0.140294 |
| V36 | 0.231417 | 0.235299 | 0.316462 | 0.324475 | 0.113609 | 0.433804 | 0.340479 | 0.326586 | 0.922190 | 0.112150 | ... | -0.099309 | 0.006961 | 0.510851 | -0.054411 | 0.031586 | -0.019032 | 0.025401 | 1.000000 | -0.039478 | 0.319309 |
| V37 | -0.494076 | -0.494043 | -0.734956 | -0.229613 | -0.031054 | -0.404817 | -0.292285 | -0.553121 | -0.045851 | -0.054827 | ... | 0.285581 | -0.256814 | -0.357785 | -0.162417 | -0.062715 | -0.006854 | -0.077991 | -0.039478 | 1.000000 | -0.565795 |
| target | 0.873212 | 0.871846 | 0.638878 | 0.512074 | 0.603984 | 0.370037 | 0.287815 | 0.831904 | 0.394767 | 0.594189 | ... | 0.123329 | 0.187311 | 0.750297 | 0.066606 | 0.077273 | -0.006034 | 0.140294 | 0.319309 | -0.565795 | 1.000000 |
33 rows × 33 columns
5.2相关性热力图
1 | |
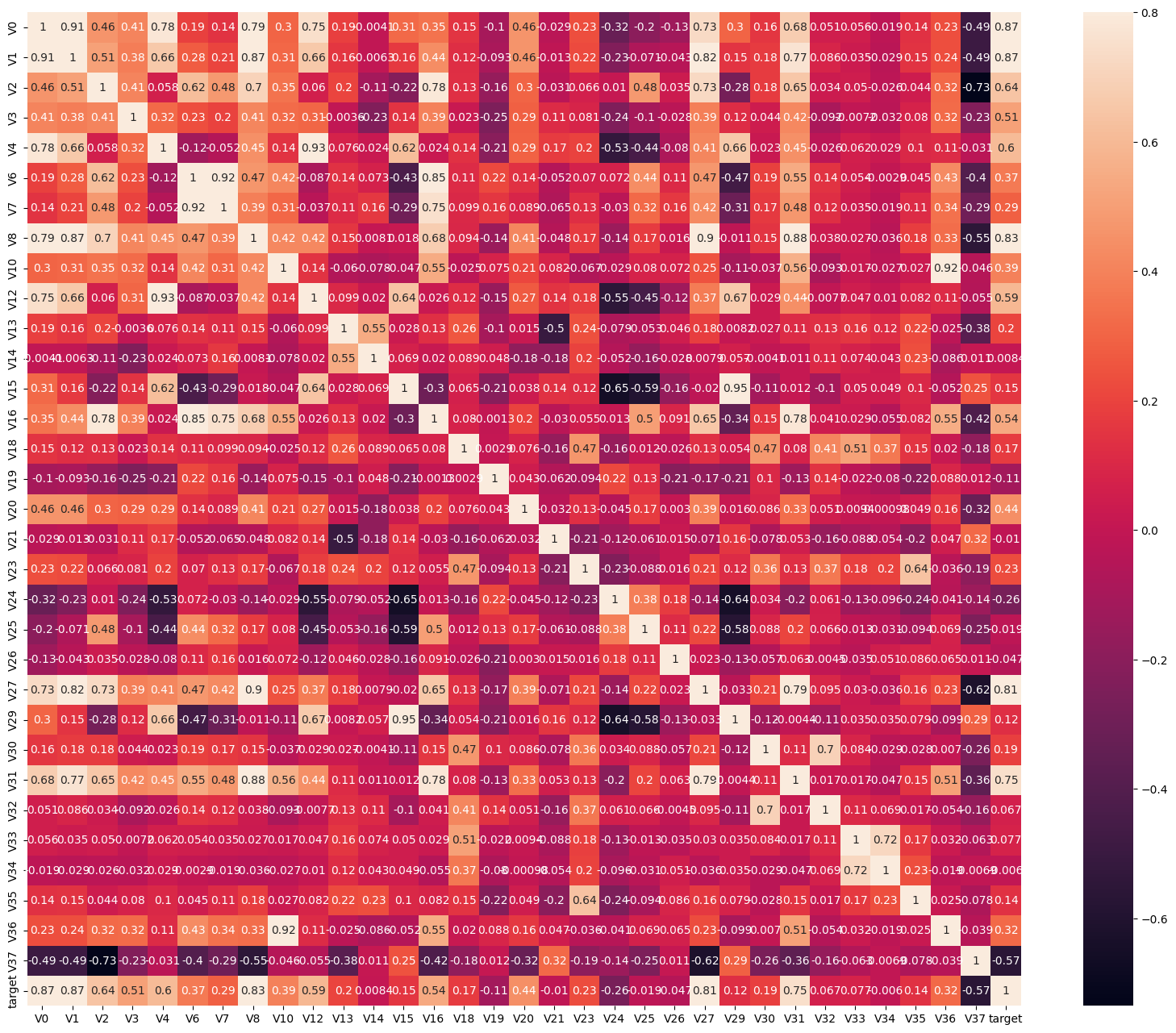
代码解释:
使用Seaborn库中的heatmap()函数来绘制相关性热力图。
ax = sns.heatmap(train_corr, vmax=.8, square=True, annot=True)在当前图像对象中绘制热力图。train_corr先前计算的相关系数矩阵。vmax参数用于设置颜色映射的最大值,即相关系数的范围。square=True将使得热力图的每个方块为正方形。annot=True表示在热力图中显示相关系数的数值。
vmax参数用于设置颜色映射的最大值,即相关系数的上限。通过将vmax设置为0.8,意味着相关系数的范围将被限制在0到0.8之间。任何具有相关系数大于0.8的值都将被映射为最浅的颜色。
通常,颜色映射是根据相关系数的值来定义的,例如,浅色可能表示正相关,深色可能表示负相关,中间色调可能表示无相关性。
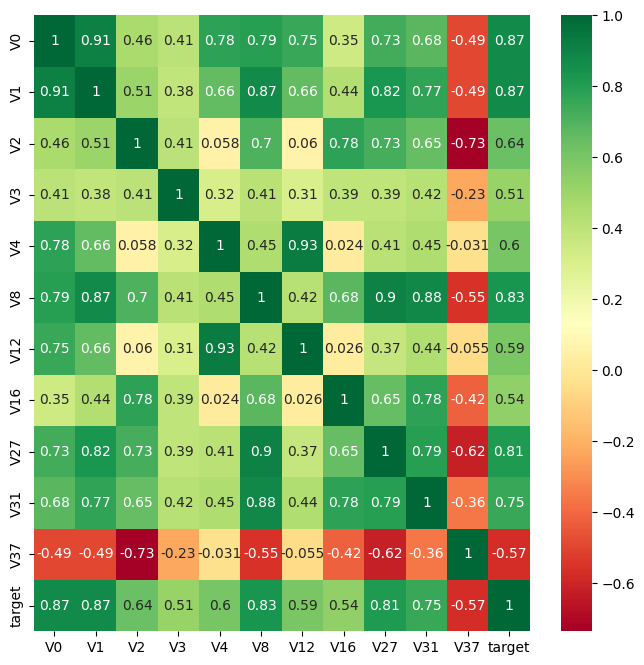
1 | |
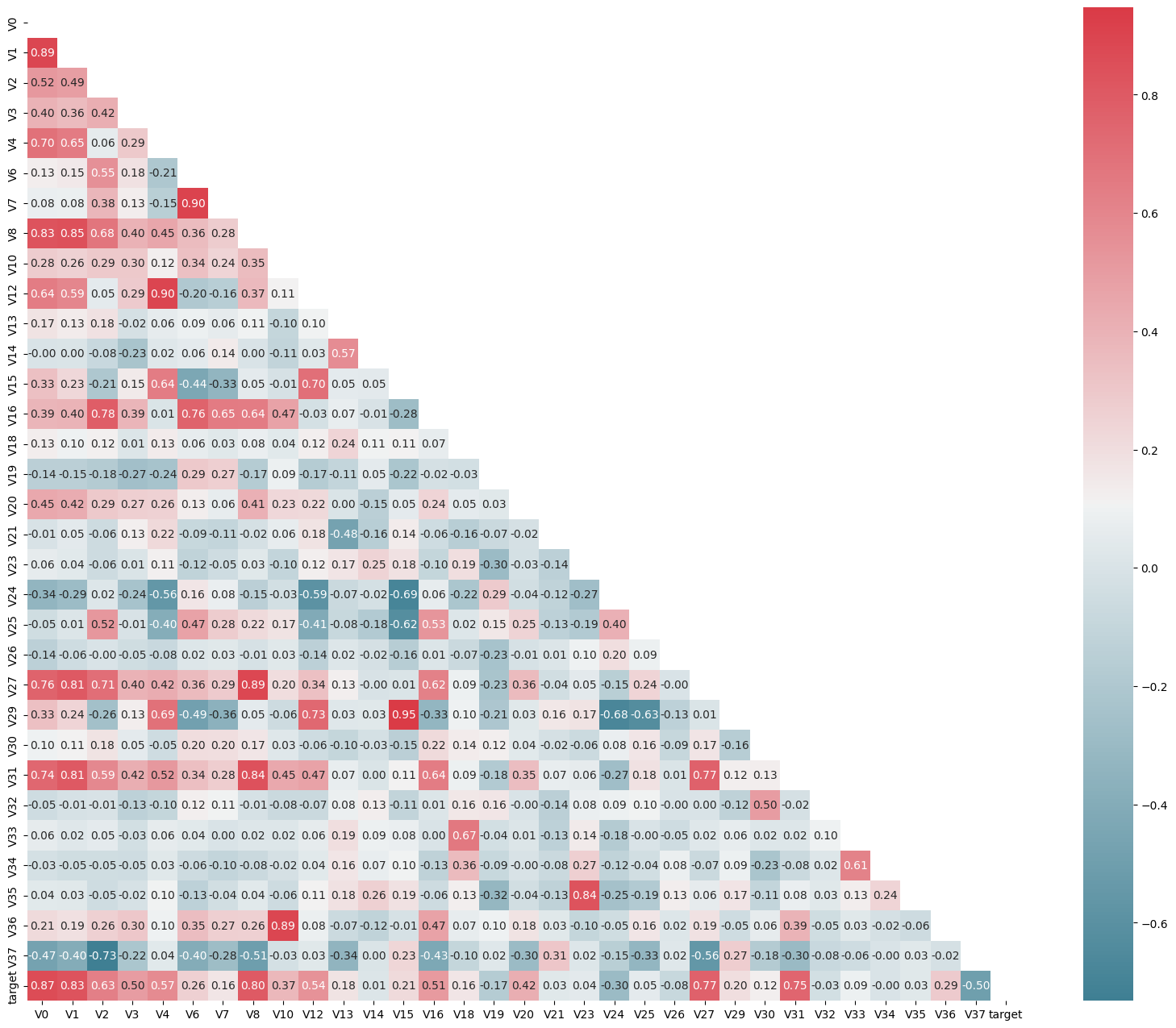
上图为所有特征变量和target变量两两之间的相关系数,由此可以看出各个特征变量V0-V37之间的相关性以及特征变量V0-V37与target的相关性。
代码详解:
mcorr = data_train1[colnm].corr(method="spearman")计算了给定变量列表[colnm]中两两变量之间的相关系数矩阵,使用Spearman秩相关系数方法,该方法更适用于非线性关系的数据,而且对异常值的影响较小。np.zeros_like(mcorr, dtype=np.bool)构建了一个与相关系数矩阵mcorr维度相同的布尔型矩阵mask,并将其所有元素初始化为False。这个矩阵mask将用于在热力图中标记需要遮挡的区域。np.zeros_like用于创建一个与给定数组(或者与给定数组形状相同)具有相同形状的全零数组。mask[np.triu_indices_from(mask)] = True将对角线右上方的元素设为True,在热力图中这些区域将被遮挡起来,只显示对角线左下方的相关系数。
np.triu_indices_from()函数用于获取一个上三角矩阵的索引。np.triu_indices_from(mask)我们可以获取 mask 矩阵中上三角区域的所有元素的索引。然后,将这些索引对应的位置在 mask 矩阵中设置为True,表示需要将相关系数矩阵中对应的元素掩盖起来。
cmap = sns.diverging_palette(220, 10, as_cmap=True)利用Seaborn库中的diverging_palette函数创建了一个颜色映射(color map)对象cmap,用于渲染热力图的颜色。
sns.diverging_palette()函数用于生成一个离散的、具有对比度的颜色调色板。它接受三个参数:start、end和as_cmap。start和end是起始颜色和结束颜色的色调值(hue),取值范围为 [0, 360]。在这里,起始颜色的色调值为 220,结束颜色的色调值为 10。这意味着生成的调色板将从蓝绿色渐变到橙红色。as_cmap=True表示将调色板转换为 colormap 对象,以便在绘图时使用。
g = sns.heatmap(mcorr, mask=mask, cmap=cmap, square=True, annot=True, fmt='0.2f')生成热力图。其中,mcorr为相关系数矩阵,mask用于指定需要遮挡的区域,cmap为颜色映射对象,square=True表示将热力图显示为正方形,annot=True表示在热力图中显示相关系数的数值,fmt='0.2f'指定数值显示格式为保留两位小数。
5.3根据相关系数筛选特征变量
以方便我们后续做特征工程及模型分析。
1 | |
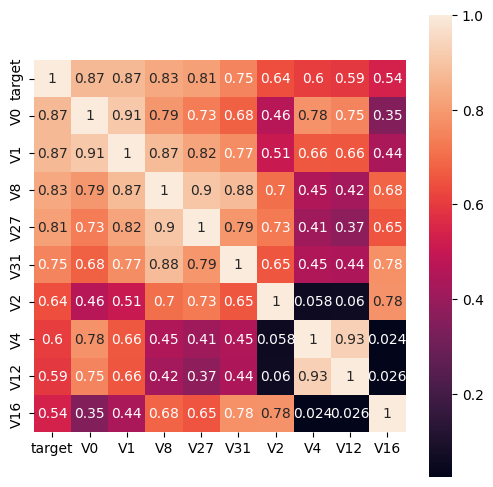
代码详解:
train_corr.nlargest(k, 'target')['target'].index用于找到与目标变量相关性最高的k个特征变量,从train_corr中找到与target相关性最高的10个变量。
nlargest(n, columns, keep='first'):n:要获取的最大值的数量。columns:指定要比较大小的列或列的列表。keep:(可选参数)设置用于处理重复值的策略。默认值为 ‘first’,表示保留第一个出现的最大值。还可以选择 ‘last’,表示保留最后一个出现的最大值。train_corr.nlargest(k, 'target')返回了一个 DataFrame,其中包含了与目标变量 ‘target’ 最相关的 K 个特征变量,返回整行。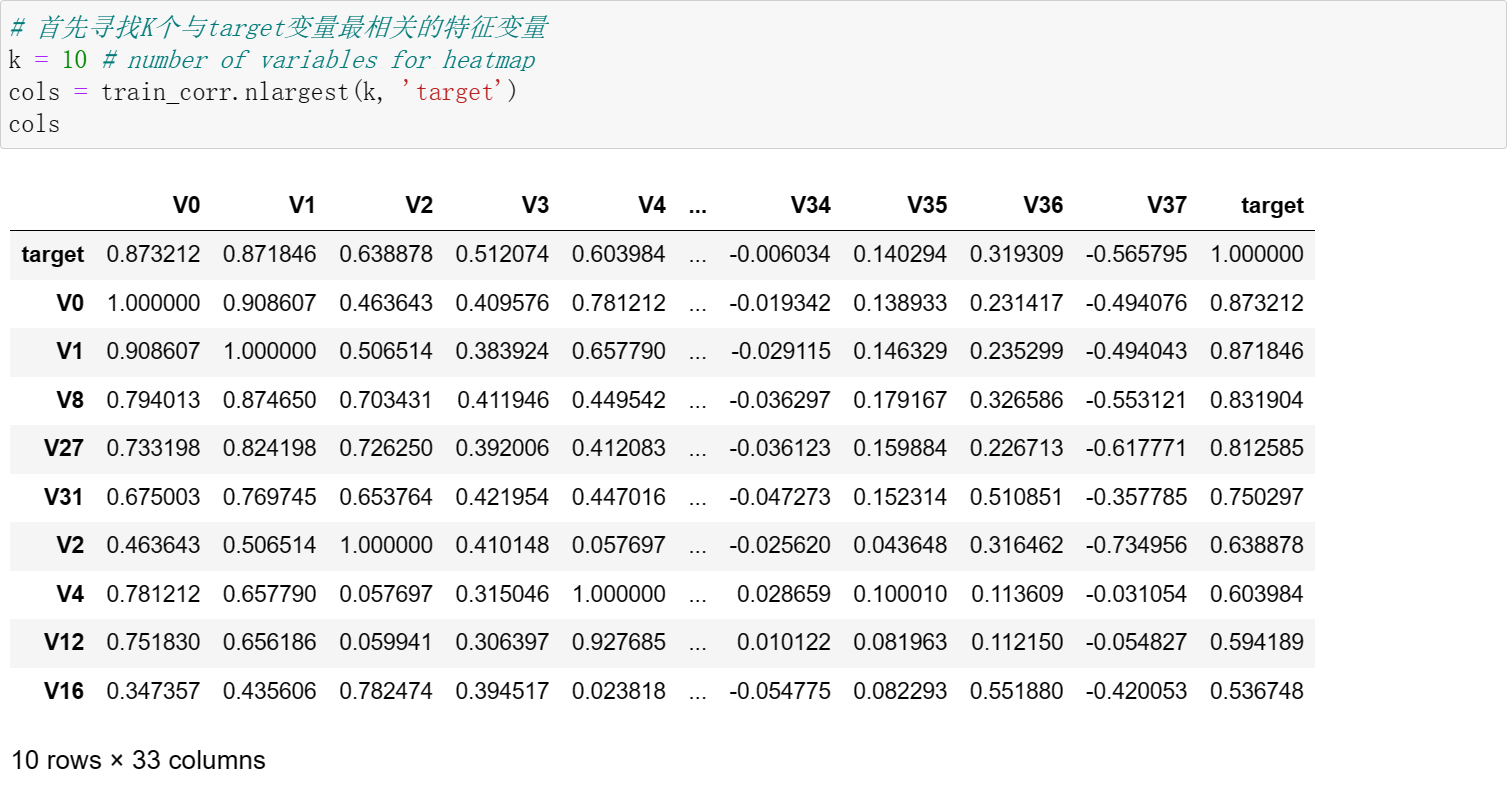
['target']从这个 DataFrame 中选择了名为 ‘target’ 的列,并返回一个 Series 对象。
.index调用了 Series 对象的 index 属性,用于获取该 Series 的索引。在这个上下文中,.index 返回了与目标变量最相关的 K 个特征变量所对应的列的索引。
np.corrcoef(train_data[cols].values.T)计算train_data中cols所对应的特征变量之间的相关系数。
corrcoef(x, y=None, rowvar=True, bias=np._NoValue, ddof=np._NoValue)函数常用的是前三个参数,x和y分别是需要计算相关系数的两个随机变量,当rowvar为True(默认情况)时,每一行代表一个随机变量,否则每一列代表一个随机变量。所以需要用.T进行转置。np.corrcoef(train_data[cols].values.T)和train_data[cols].corr()返回的数值都是一样的。最主要的区别是前者返回的类型是NumPy 数组,后者为 Pandas DataFrame
hm1 = sns.heatmap(cm, cbar=True, annot=True, square=True)# cbar=True 添加颜色条(color bar)来表示相关系数的范围。g = sns.heatmap(train_data[cols].corr(),annot=True,square=True,cmap="RdYlGn")cmap=”RdYlGn” 指定颜色映射为 “RdYlGn”。
1 | |
代码解释:
corrmat["target"]:从相关性矩阵corrmat中选择名为 “target” 的列,得到一个包含所有特征与目标变量的相关系数的 Series 对象。abs(corrmat["target"]) > threshold:计算相关系数的绝对值,并将结果与阈值threshold进行比较,得到一个布尔类型的 Series 对象,表示哪些特征与目标变量的相关系数大于阈值。corrmat.index[abs(corrmat["target"])>threshold]:根据上述布尔索引,从相关性矩阵的索引中选择相应的特征名。这将得到一个包含与目标变量的相关系数大于阈值的特征名的索引对象。.index[]返回索引值。
可以发现,与target变量的相关系数大于0.5的特征变量被直观地筛选出来。这一方法可以简单、直观地判断哪些特征变量线性相关,相关系数越大,就认为这些特征变量对target变量的线性影响越大。
说明:相关性选择主要用于判别线性相关对于target变量如果存在更复杂的函数形式的影响则建议使用树模型的特征重要性去选择
1 | |
由于’V14’, ‘V21’, ‘V25’, ‘V26’, ‘V32’, ‘V33’, ‘V34’特征的相关系数值小于0.5,故认为这些特征与最终的预测target值不相关,删除这些特征变量;其可以发现一些不重要的特征并快速删除,方便快速分析重要特征。这里先不删除这些特征(注释的代码行用于删除特征),因为后续分析还会用到。
5.4Box-Cox变换
由于线性回归是基于正态分布的,因此在进行统计分析时,需要转换数据使其符合正态分布。
Box-Cox 变换是一种常见的数据转换技术,用于将非正态分布的数据转换为近似正态分布的数据。这一变换可以使线性回归模型在满足线性、正态性、独立性及方差齐性的同时,又不丢失信息。在对数据做Box-Cox变换之后,可以在一定程度上减小不可观测的误差和预测变量的相关性,这有利于线性模型的拟合及分析出特征的相关性。
在做Box-Cox变换之前,需要对数据做归一化预处理。在归一化时,对数据进行合并操作可以使训练数据和测试数据一致。这种方式可以在线下分析建模中使用,而线上部署只需采用训练数据的归一化即可。
1 | |
| V0 | V1 | V2 | V3 | V4 | V6 | V7 | V8 | V10 | V12 | ... | V27 | V29 | V30 | V31 | V32 | V33 | V34 | V35 | V36 | V37 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0.566 | 0.016 | -0.143 | 0.407 | 0.452 | -1.812 | -2.360 | -0.436 | -0.940 | -0.073 | ... | 0.168 | 0.136 | 0.109 | -0.615 | 0.327 | -4.627 | -4.789 | -5.101 | -2.608 | -3.508 |
| 1 | 0.968 | 0.437 | 0.066 | 0.566 | 0.194 | -1.566 | -2.360 | 0.332 | 0.188 | -0.134 | ... | 0.338 | -0.128 | 0.124 | 0.032 | 0.600 | -0.843 | 0.160 | 0.364 | -0.335 | -0.730 |
| 2 | 1.013 | 0.568 | 0.235 | 0.370 | 0.112 | -1.367 | -2.360 | 0.396 | 0.874 | -0.072 | ... | 0.326 | -0.009 | 0.361 | 0.277 | -0.116 | -0.843 | 0.160 | 0.364 | 0.765 | -0.589 |
| 3 | 0.733 | 0.368 | 0.283 | 0.165 | 0.599 | -1.200 | -2.086 | 0.403 | 0.011 | -0.014 | ... | 0.277 | 0.015 | 0.417 | 0.279 | 0.603 | -0.843 | -0.065 | 0.364 | 0.333 | -0.112 |
| 4 | 0.684 | 0.638 | 0.260 | 0.209 | 0.337 | -1.073 | -2.086 | 0.314 | -0.251 | 0.199 | ... | 0.332 | 0.183 | 1.078 | 0.328 | 0.418 | -0.843 | -0.215 | 0.364 | -0.280 | -0.028 |
5 rows × 32 columns
1 | |
| V0 | V1 | V2 | V3 | V4 | V6 | V7 | V8 | V10 | V12 | ... | V27 | V29 | V30 | V31 | V32 | V33 | V34 | V35 | V36 | V37 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| count | 4813.000000 | 4813.000000 | 4813.000000 | 4813.000000 | 4813.000000 | 4813.000000 | 4813.000000 | 4813.000000 | 4813.000000 | 4813.000000 | ... | 4813.000000 | 4813.000000 | 4813.000000 | 4813.000000 | 4813.000000 | 4813.000000 | 4813.000000 | 4813.000000 | 4813.000000 | 4813.000000 |
| mean | 0.694172 | 0.721357 | 0.602300 | 0.603139 | 0.523743 | 0.748823 | 0.745740 | 0.715607 | 0.348518 | 0.578507 | ... | 0.881401 | 0.388683 | 0.589459 | 0.792709 | 0.628824 | 0.458493 | 0.483790 | 0.762873 | 0.332385 | 0.545795 |
| std | 0.144198 | 0.131443 | 0.140628 | 0.152462 | 0.106430 | 0.132560 | 0.132577 | 0.118105 | 0.134882 | 0.105088 | ... | 0.128221 | 0.133475 | 0.130786 | 0.102976 | 0.155003 | 0.099095 | 0.101020 | 0.102037 | 0.127456 | 0.150356 |
| min | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | ... | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 |
| 25% | 0.626676 | 0.679416 | 0.514414 | 0.503888 | 0.478182 | 0.683324 | 0.696938 | 0.664934 | 0.284327 | 0.532892 | ... | 0.888575 | 0.292445 | 0.550092 | 0.761816 | 0.562461 | 0.409037 | 0.454490 | 0.727273 | 0.270584 | 0.445647 |
| 50% | 0.729488 | 0.752497 | 0.617072 | 0.614270 | 0.535866 | 0.774125 | 0.771974 | 0.742884 | 0.366469 | 0.591635 | ... | 0.916015 | 0.375734 | 0.594428 | 0.815055 | 0.643056 | 0.454518 | 0.499949 | 0.800020 | 0.347056 | 0.539317 |
| 75% | 0.790195 | 0.799553 | 0.700464 | 0.710474 | 0.585036 | 0.842259 | 0.836405 | 0.790835 | 0.432965 | 0.641971 | ... | 0.932555 | 0.471837 | 0.650798 | 0.852229 | 0.719777 | 0.500000 | 0.511365 | 0.800020 | 0.414861 | 0.643061 |
| max | 1.000000 | 1.000000 | 1.000000 | 1.000000 | 1.000000 | 1.000000 | 1.000000 | 1.000000 | 1.000000 | 1.000000 | ... | 1.000000 | 1.000000 | 1.000000 | 1.000000 | 1.000000 | 1.000000 | 1.000000 | 1.000000 | 1.000000 | 1.000000 |
8 rows × 32 columns
代码解释:
cols_numeric=list(data_all.columns)- 将
data_all中的所有列名保存在cols_numeric列表中。
- 将
def scale_minmax(col):- 定义
scale_minmax的函数,输入参数col表示数据的某一列。即使传入的是整个列,Pandas库的向量化操作会自动将这些操作应用到列中的每个元素上,从而实现对每个元素的归一化处理。
- 定义
return (col-col.min())/(col.max()-col.min())- 计算数据列
col的归一化值。它用数据列中每个元素减去该列的最小值,然后除以该列的最大值与最小值之差,从而实现归一化处理。
- 计算数据列
data_all[cols_numeric] = data_all[cols_numeric].apply(scale_minmax,axis=0)- 进行广播,将归一化处理的结果应用到
data_all数据框的所有数值型列上。 data_all[cols_numeric]表示选择data_all数据框中cols_numeric列表中的列。.apply(scale_minmax, axis=0)将scale_minmax函数应用到每列数据上,并指定axis=0以逐列进行操作。
- 进行广播,将归一化处理的结果应用到
也可以分开对训练数据和测试数据进行归一化处理,不过这种方式需要建立在训练数据和测试数据分布一致的前提下,建议在数据量大的情况下使用(数据量大,一般分布比较一致),能加快归一化的速度。而数据量较小会存在分布差异较大的情况,此时,在数据分析和线下建模中应该将数据统一归一化。
1 | |
1 | |
1 | |

代码详解:
plt.title():这是Matplotlib库中的一个函数,用于设置当前子图的标题。它接受一个字符串作为参数,表示要设置的标题内容。'skew=' + '{:.4f}'.format(stats.skew(dat[var])):这是一个字符串格式化操作,用于构造标题内容。其中包含了以下几个部分:'skew=':这是一个固定的字符串,用于标识标题内容中的部分。'{:.4f}':这是一个格式化字符串,表示将要显示的数值(即偏度值)的格式。{:.4f}中的4表示小数点后四位,.f表示浮点数。format(stats.skew(dat[var])):这是一个格式化操作,用于将实际的数值(stats.skew(dat[var]))应用到格式化字符串中。
stats.skew(dat[var]):这是SciPy库中的stats.skew()函数,用于计算给定数据集(dat[var])的偏度值。偏度是衡量数据分布偏斜程度的统计量,负值表示左偏(左侧的尾部更长),正值表示右偏(右侧的尾部更长),0表示对称分布。
{:.4f}是一种格式化字符串的方法,用于将浮点数进行格式化输出。
具体用法:
{}:花括号内放置要格式化的值的占位符。::表示格式说明符的开始。.4f:表示使用浮点数格式化,并保留小数点后四位。
:的用处:- 在格式说明符中,冒号(
:)用来分隔格式说明符的各个部分。 - 在
{}内的冒号后面,可以添加格式说明符,对应要格式化的值按照指定的格式输出。
- 在格式说明符中,冒号(
中间可以填哪些参数,表示什么:
- 宽度参数:如
{:<10}表示左对齐并占用 10 个字符的宽度。 - 对齐参数:如
{:>10}表示右对齐并占用 10 个字符的宽度。 - 精度参数:如
{:.2f}表示保留两位小数。 - 类型参数:如
{:s}表示字符串类型,{:d}表示整数类型,{:f}表示浮点数类型等。
- 宽度参数:如
总结起来,冒号(:)在格式化字符串中的作用是分隔格式说明符的各个部分。精度参数和类型参数是冒号后面的部分,用于指定格式化的精度和类型。
[0][1] 是用于获取 np.corrcoef(dat[var],dat['target']) 返回的相关系数矩阵中的特定元素的索引表示方式。
np.corrcoef(dat[var], dat['target']) 用于计算 dat[var] 和 dat['target'] 之间的相关系数矩阵。
- 相关系数矩阵是一个二维矩阵,其中每个元素是两个变量之间的相关系数。例如:

- 在这种情况下,
[0][1]表示相关系数矩阵的第一行第二列的元素。其中,第一行对应于dat[var]与dat[var]自身的相关系数,而第二列对应于dat[var]与dat['target']的相关系数。
因此,plt.title('corr='+'{:.2f}'.format(np.corrcoef(dat[var],dat['target'])[0][1])) 中的 [0][1] 表示提取相关系数矩阵中与 dat[var] 与 dat['target'] 相关系数对应的值,并将其格式化为小数点后两位的字符串。
1 | |
