机器学习06-推荐系统
基于内容的推荐算法
假设您经营一家大型电影流媒体网站,用户使用一到五颗星对电影进行评级,请预测用户未看过的电影可能给出的评分。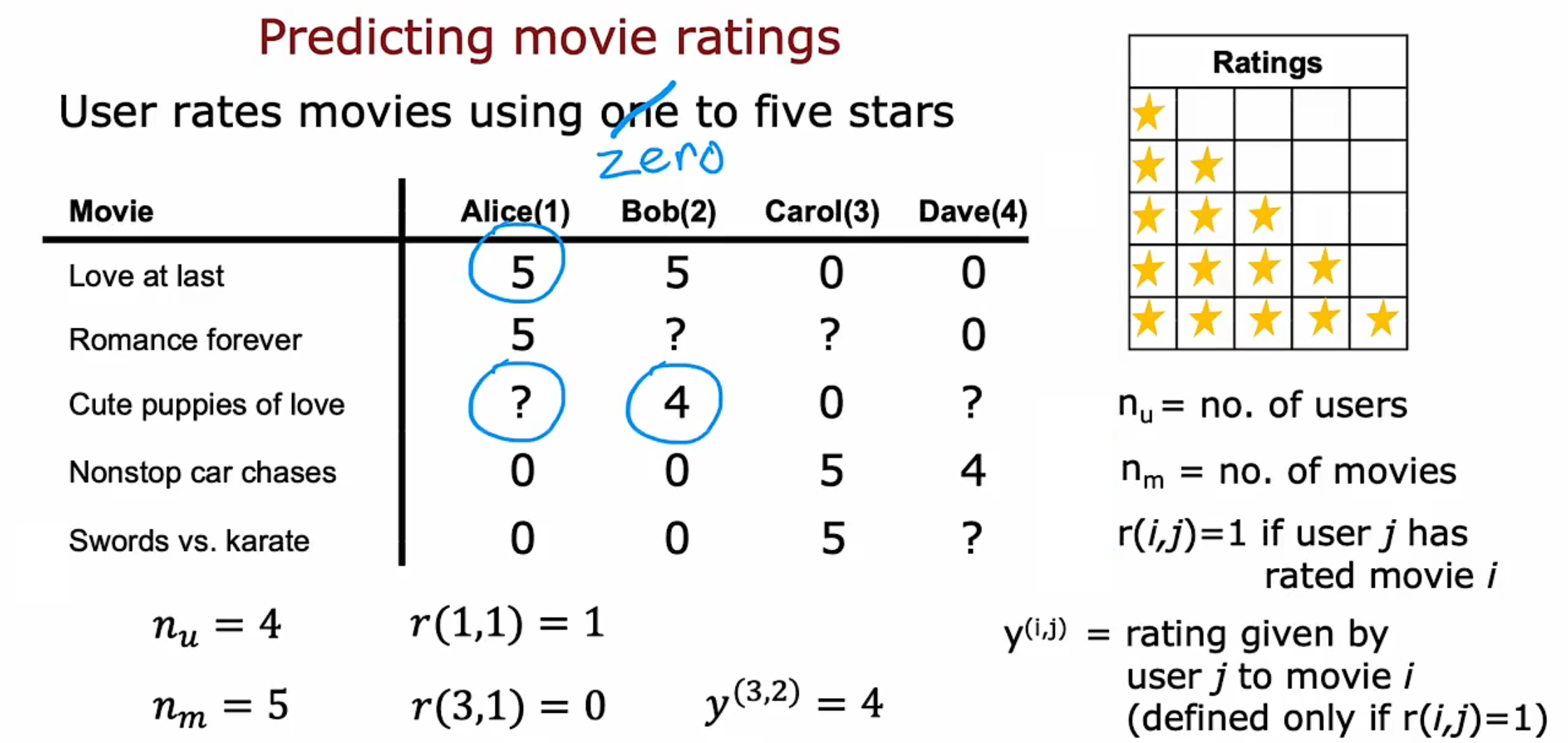
$n_u$ :用户数量
$n_m$ :电影数量
$r(i,j)$ = 1 :第j个用户对 第i个电影做出评价
$y^{(i,j)}$ :当 $r(i,j)$ = 1时,第j个用户对第i个电影的评分
假设每一部电影都有一个特征集X,n表示特征数量,$x_1$ 衡量一部电影为爱情片的程度,$x_2$ 衡量一部电影为动作片的程度,例如 $x^{(1)}=\begin{bmatrix}0.9\0\end{bmatrix}$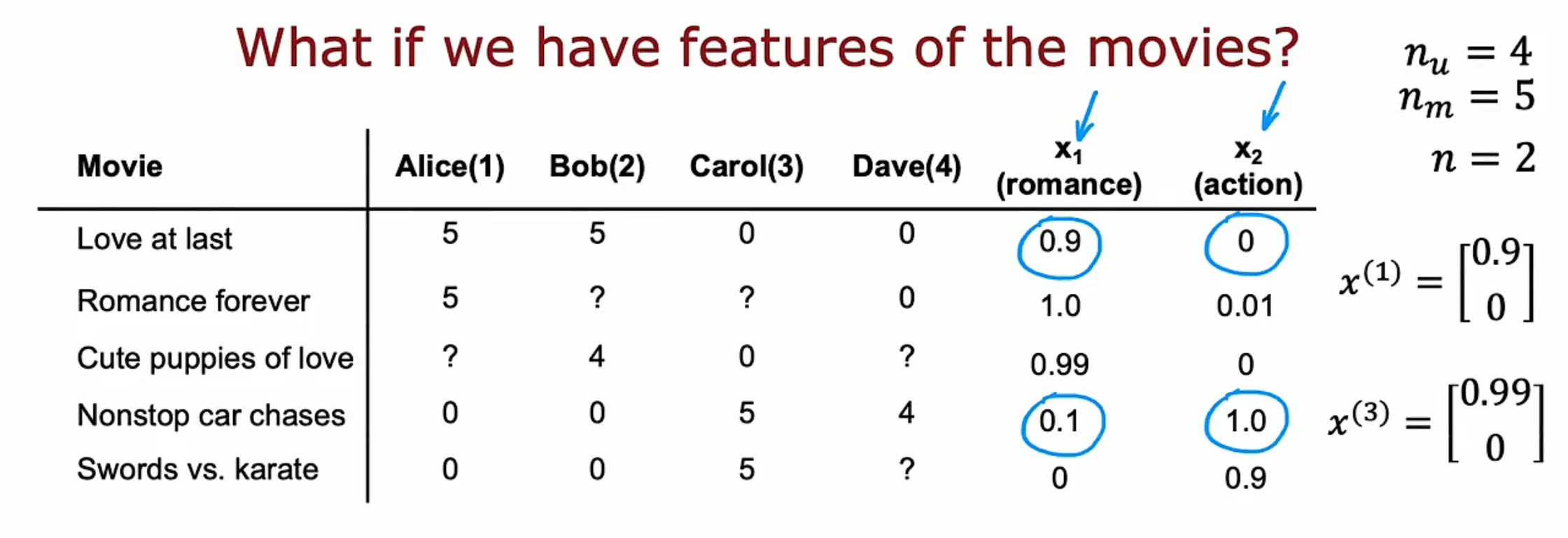
我们可以把每一个用户的预测评价值当做线性回归问题。对于每个用户 j,需要学习参数 $w$ 和 $b$ , 之后便可用 $w · x^{(i)} + b$ 预测用户 j 对电影 i 的评分。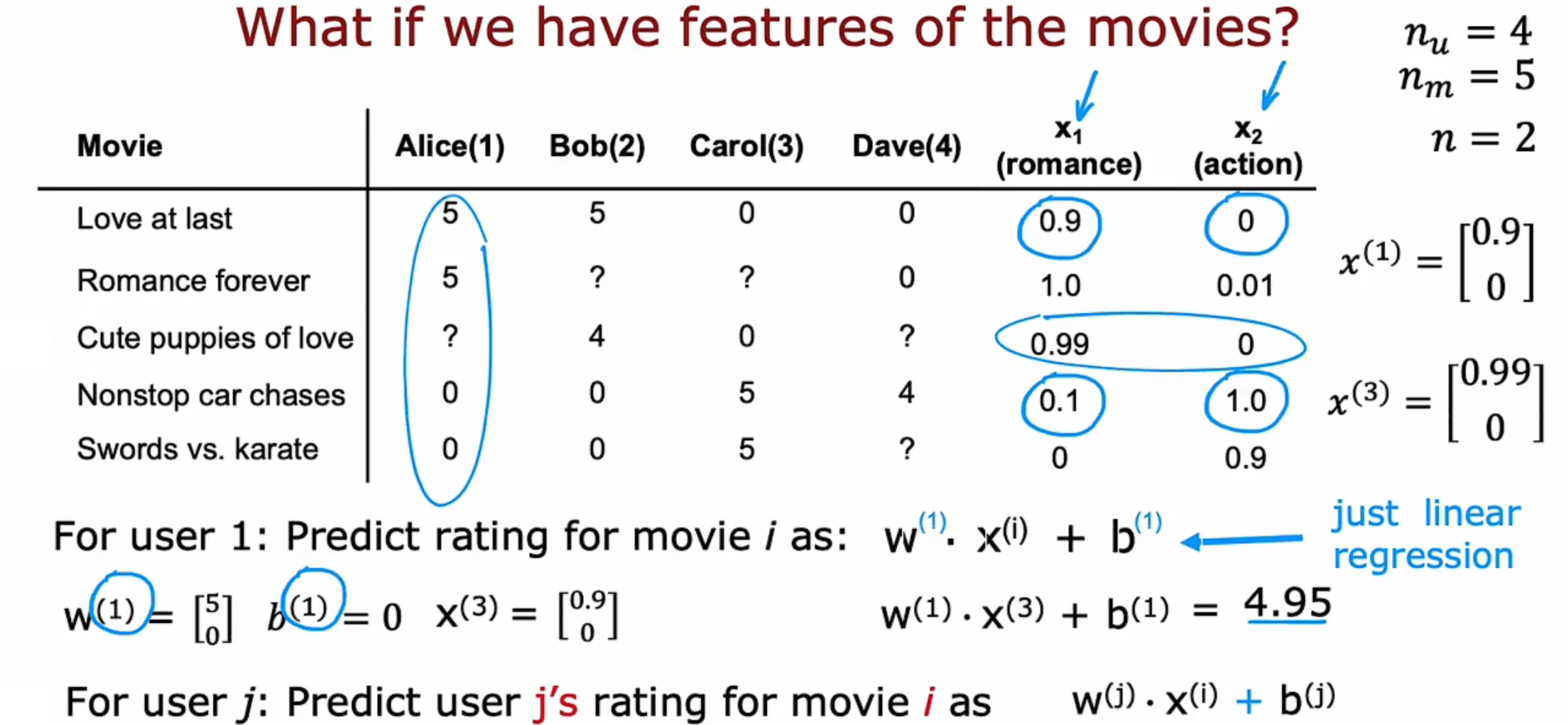
例如,预测用户 1 对电影 3 的评分,假设模型各参数为$\mathbf{w}^{(1)}=\begin{bmatrix}5\0\end{bmatrix} \quad b^{(1)}=0\quad\mathbf{x}^{(3)}=\begin{bmatrix}0.9\0\end{bmatrix}$ ,则有 $\mathbf{w}^{(1)}\cdot\mathbf{x}^{(3)}+\mathbf{b}^{(1)}=4.95$
一般的,用户j对电影i的评分为:$\mathbf{w^{(j)}\cdot x^{(i)}+b^{(j)}}$
成本函数

其中,$\sum_{i:r(i,j)=1}$ 表示仅对$r(i,j)$ = 1 的值求和。使用正则化后的代价函数为:
$$
\min_{w^{(j)}b^{(j)}}{J}(w^{(j)},b^{(j)})=\frac{1}{2m^{(j)}}\sum_{i:r(i,j)=1}(w^{(j)}\cdot x^{(i)}+b^{(j)}-y^{(i,j)})^{2} +\frac{\lambda}{2m^{(j)}}\sum_{k=1}^{n}\left(w_{k}^{(j)}\right)^{2}
$$
为了使式子更简单,可以去掉 $\frac{1}{2m^{(j)}}$ 中的 $m^{(j)}$ ,去掉后值不变。
对所有的用户:
预测电影特征
基于内容的推荐算法要求取得每部电影的特征值,然而这是很难的。对此,有另外一种算法无需取得特征值,而只要根据用户的爱好矩阵 便可预测出用户对电影的评分。
在之前的基于内容的推荐系统中,对于每一部电影,我们都掌握了可用的特征,比如衡量一部电影为爱情片的程度、动作片的程度,使用这些特征训练来出每一个用户的参数。相反地,如果我们拥有用户的参数,我们可以学习得出电影的特征。
假设拥有所有四个用户的参数,如下,进而我们可以求出电影的特征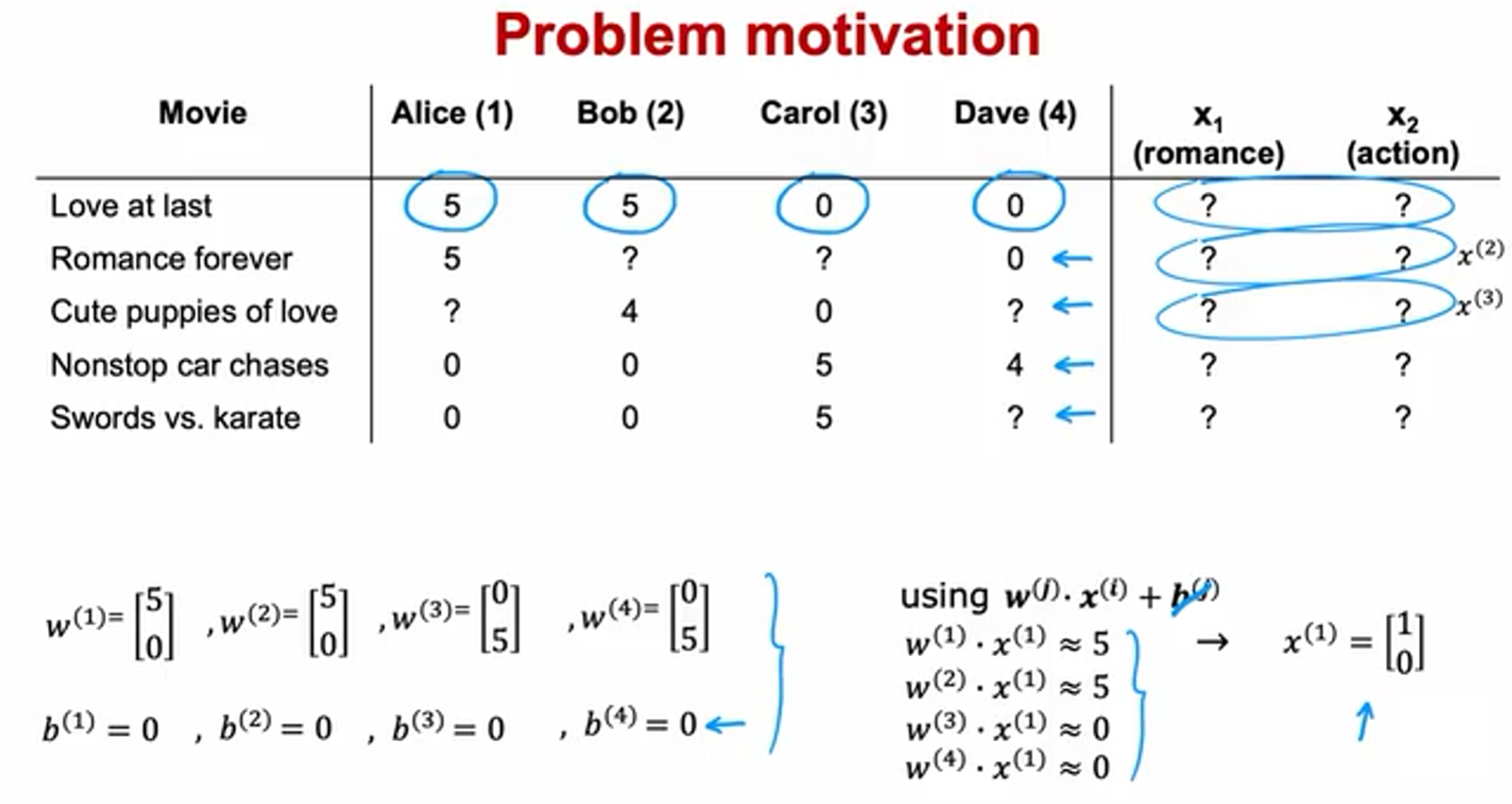
成本函数

一部电影特征的成本函数:
$$
J(x^{i})=\frac{1}{2}\sum_{j:r(i,j)=1}(w^{(j)}\cdot x^{(i)}+b^{(j)}-y^{(i,j)})^2+\frac{\lambda}{2}\sum_{k=1}^{n}\left(x_k^{(i)}\right)^2
$$
所有电影特征的成本函数:
$$
J\left(x^{(1)},x^{(2)},…,x^{(n_m)}\right)=\frac12\sum_{i=1}^{n_m}\sum_{j:r(i,j)=1}\left(w^{(j)}\cdot x^{(j)}+b^{(j)}-y^{(i,j)}\right)^2+\frac\lambda2\sum_{i=1}^{n_m}\sum_{k=1}^n\left(x_k^{(i)}\right)^2
$$
协同过滤算法
目前我们都是在假设已有用户参数的基础上来预测电影特征的,但是这些参数从哪里得到呢?我们将基于内容的推荐算法(学习w和b)和预测电影特征算法(学习x)结合在一起,这就是协同过滤算法 。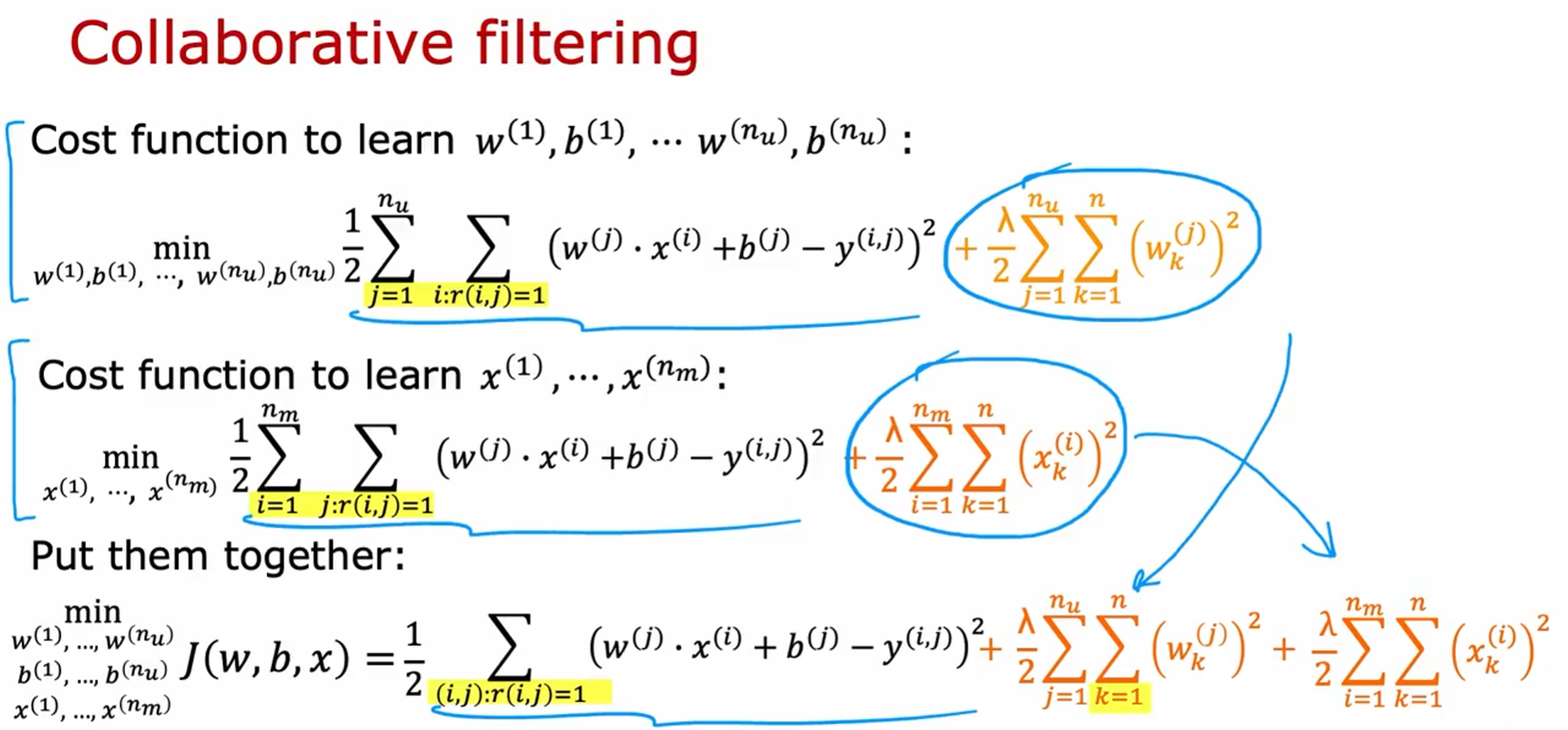
上面是逐列遍历矩阵中非零元素,下面试逐行遍历矩阵中非零元素
成本函数
$$
\min_{b^{(1)},…,b^{(n_{u})}}J(w,b,x)=\frac{1}{2}\sum_{(i,j):r(i,j)=1}\left(w^{(j)}\cdot x^{(j)}+b^{(j)}-y^{(i,j)}\right)^{2}+\frac{\lambda}{2}\sum_{j=1}^{n_{u}}\sum_{k=1}^{n}\left(w_{k}^{(j)}\right)^{2}+\frac{\lambda}{2}\sum_{i=1}^{n_{m}}\sum_{k=1}^{n}\left(x_{k}^{(j)}\right)^{2}
$$
梯度下降

在协同过滤中,是因为有多个用户评价同一部电影,了解这部电影可能是什么样子,所以可以预测出电影特征。
推广至二进制标签:收藏、喜欢和点击

均值归一化
让我们来看下面的用户评分数据: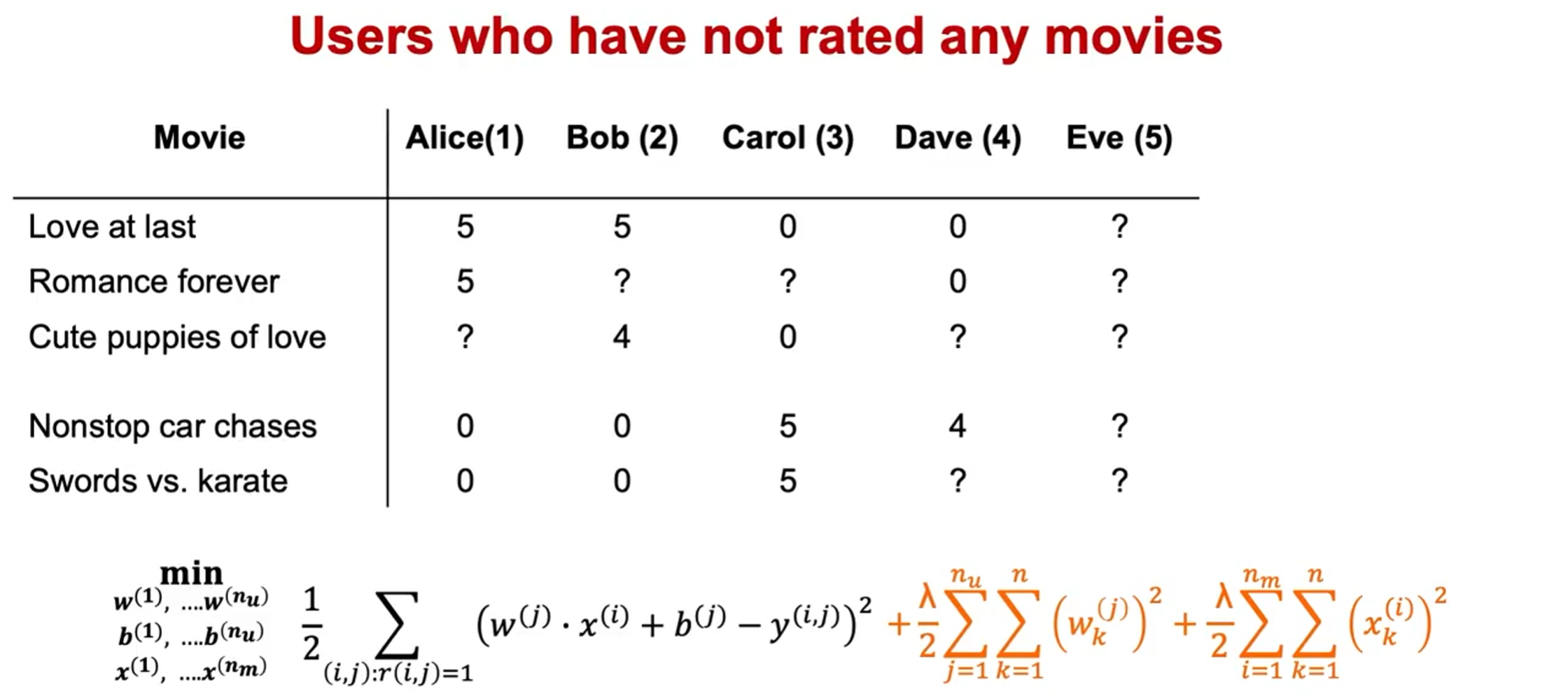
如果我们新增一个用户 Eve,并且 Eve 没有为任何电影评分,那么我们以什么为依据为Eve推荐电影呢?
如果这个数据集上运行算法,会得到Eve的参数为$w^{(5)}=\begin{bmatrix}0\0\end{bmatrix}\quad b^{(5)}=0$
,预测结果都为0。
因此,如果有一个尚未对任何内容进行评分的新用户,算法会认为他们会对所有电影都是零星评分,这样的预测并不是非常合理的。
因此,我们将使用均值归一化帮助该算法为尚未对任何电影进行评级的新用户更好地预测电影评级。
我们首先需要对结果矩阵进行均值归一化处理,将每一个用户对某一部电影的评分减去所有用户对该电影评分的平均值: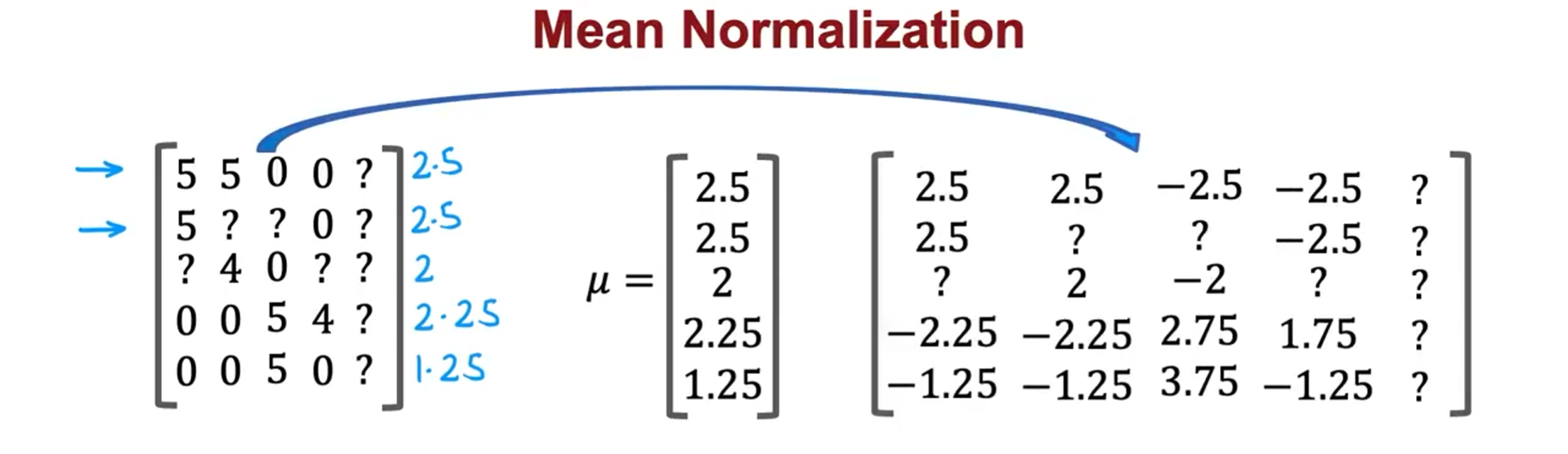
然后我们利用这个新的 矩阵来训练算法。 如果我们要用新训练出的算法来预测评分,则需要将平均值重新加回去,预测$w^{(j)}\cdot x^{(i)}+b^{(j)}+\mu_i$
对于Eve,我们的新模型会认为她给每部电影的评分都是该电影的平均分。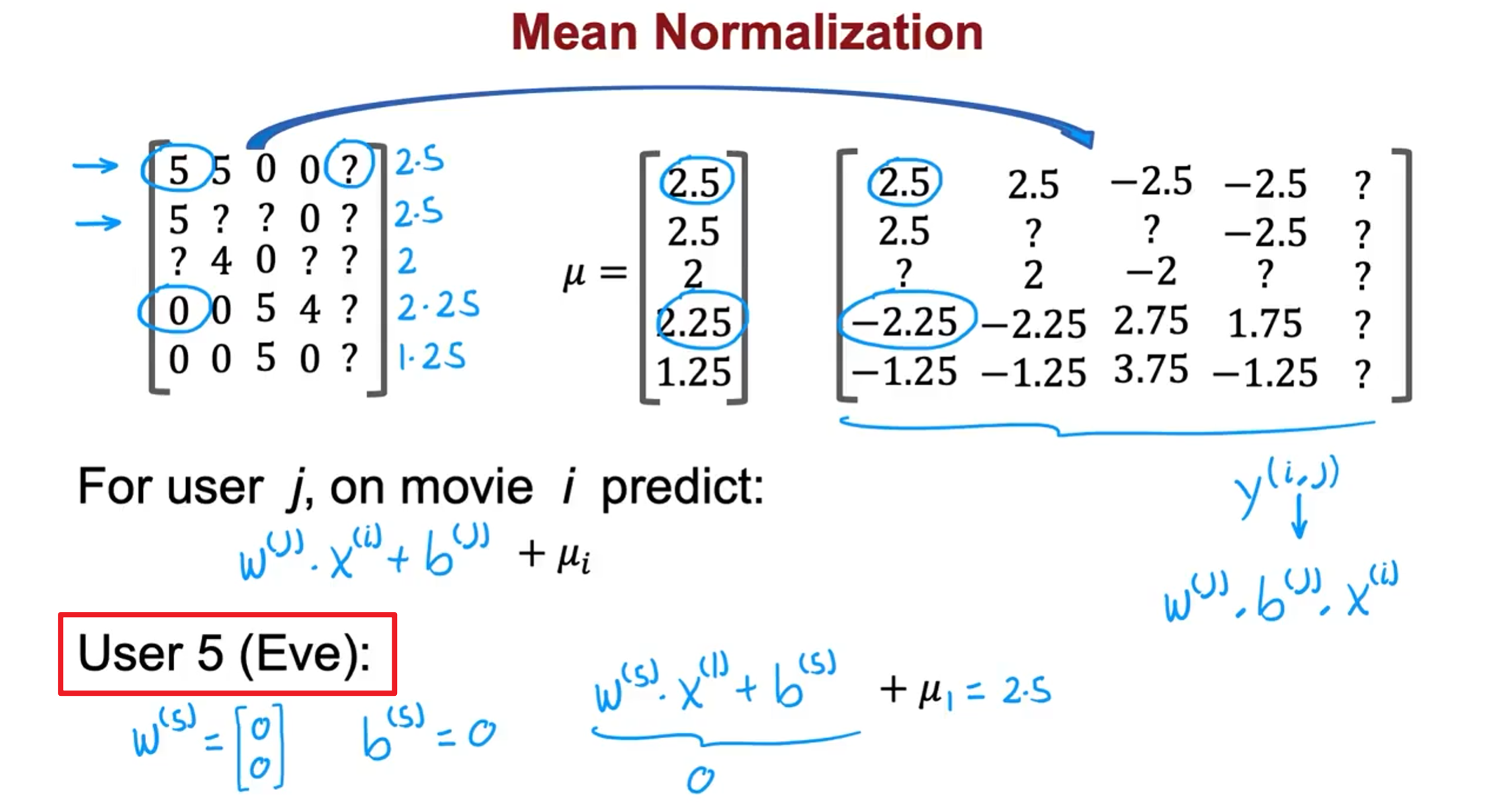
均值归一化使算法更快,更重要的是,当用户评价的电影很少甚至根本没有电影时,它可以让算法给出更好、更合理的预测。
寻找相关特征
当你浏览一些电影时,平台会给你推荐一些相似的电影,这是如何做到的?
使用算法学习出电影的特征 $X^i$ ,要是想要找出其他与 $X^i$ 相似的电影,即尝试找到具有特征 $X^k$ 的电影,并且 $X^k$ 类似于 $X^i$ 。我们用以下方法确定电影特征之间的相似程度:
$$
\sum_{l=1}^n\left(x_l^{(k)}-x_l^{(i)}\right)^2
$$
协同过滤的局限性
冷启动问题。如何解决
- 对很少有用户评价的新项目进行排名?
- 向对很少项目进行评分的新用户显示一些合理的内容?
使用有关电影或用户的辅助信息:
- 电影:类型、电影明星、工作室 …
- 用户:人口统计数据(年龄、性别、地点)、偏好 …
基于内容的协同过滤
协同过滤VS基于内容的协同过滤
协同过滤:
- 根据与你评分相近的用户的评分向你推荐商品
基于内容的协同过滤:
- 根据用户和物品的特征向您推荐物品,找到合适的匹配
用户和项目特性示例
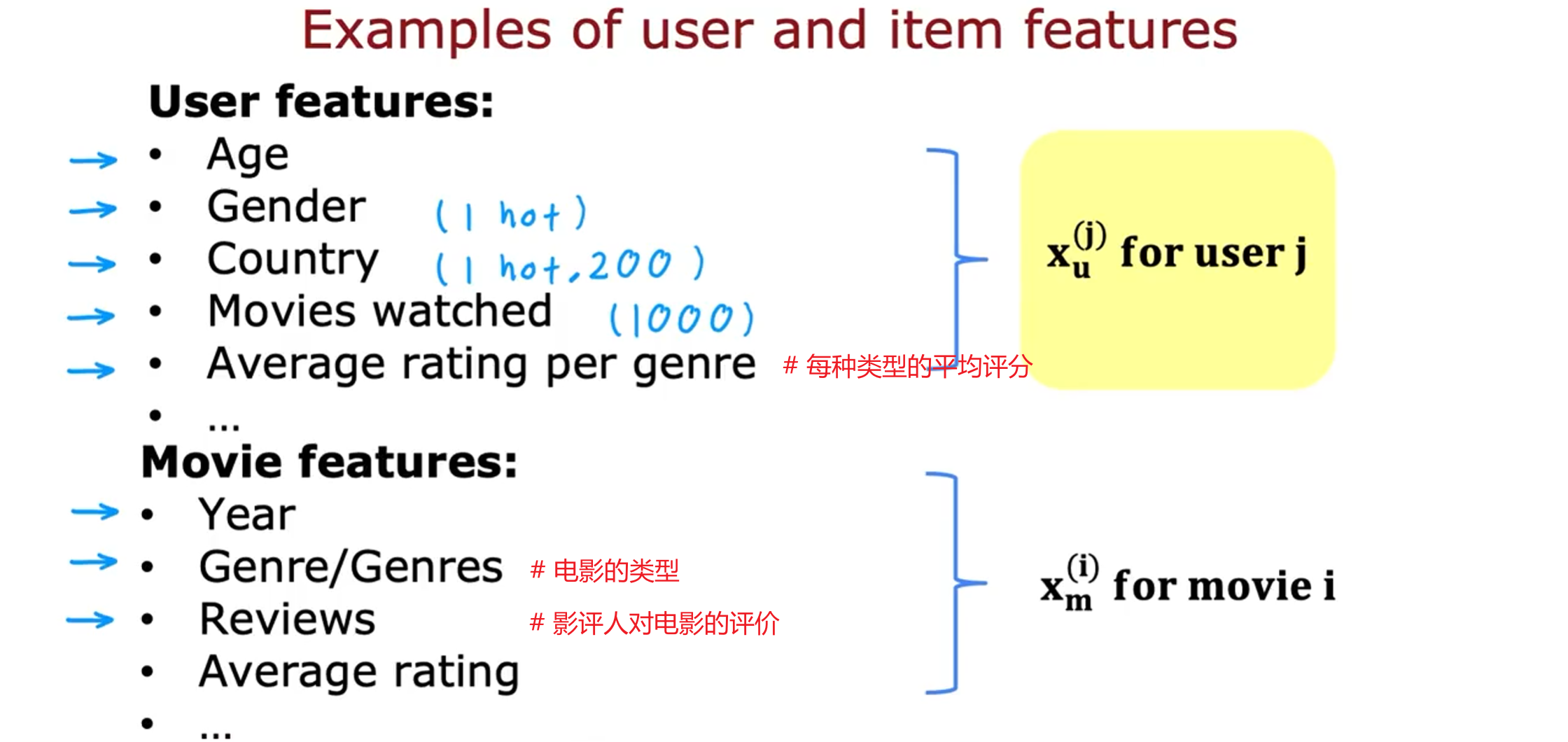
用户特征和电影特征的大小可能会有很大的差距。例如,用户特征可能会有1500个,而电影特征可能只会有50个。
匹配用户和电影
之前我们用 $w^{(j)}\cdot x^{(i)}+b^{(j)}$ 来预测用户j对电影i的评分,在此,我们用 $V_u^J\cdot V_m^i$ 来预测用户j对电影i的评分。
$b$ :去掉b不会影响算法性能
$V_u^J$ :代表向量,是根据用户j的特征 $X_u^j$ 计算的数字列表,下标u代表用户
$V_m^i$ :代表向量,是根据电影i的特征 $X_m^i$ 计算的数字列表,下标m代表电影
例如,$\mathbf{V_u}=\begin{bmatrix}4.9\0.1\\vdots\3.0\end{bmatrix}$ ,第一个数字代表用户对爱情电影的喜爱程度,第二个代表对动作电影的喜爱程度;$\mathrm{Vm}=\begin{bmatrix}4.5\0.2\\vdots\3.5\end{bmatrix}$ ,第一个数字表示电影包含爱情片元素的程度,第二个表示包含动作片元素的程度。$V_u\cdot V_m$ 进行点积即可了解用户对该电影的喜爱程度。
点积需要$V_u$ 和 $V_m$ 有相同的维度,比如都需要有32个数字。但是,$V_u$ 和 $V_m$ 是根据用户特征$X_u^j$ 和电影特征$X_m^i$ 计算来的,用户特征和电影特征不一定有相同大小。
总而言之,在协同过滤中,我们有许多用户对不同的项目进行评分。在基于内容的过滤中,我们有用户的特征和项目的特征,我们想找到一种方法来找到用户和项目之间的良好匹配。
基于内容过滤的深度学习方法
我们给定用户特征$X_u^j$ 和电影特征$X_m^i$ ,计算向量$V_u$ 和 $V_m$ 最好的办法是利用神经网络。
我们将用户特征$X_u^j$ 和电影特征$X_m^i$ 作为输入,将$V_u$ 和 $V_m$ 作为输出,最后计算$V_u\cdot V_m$ 。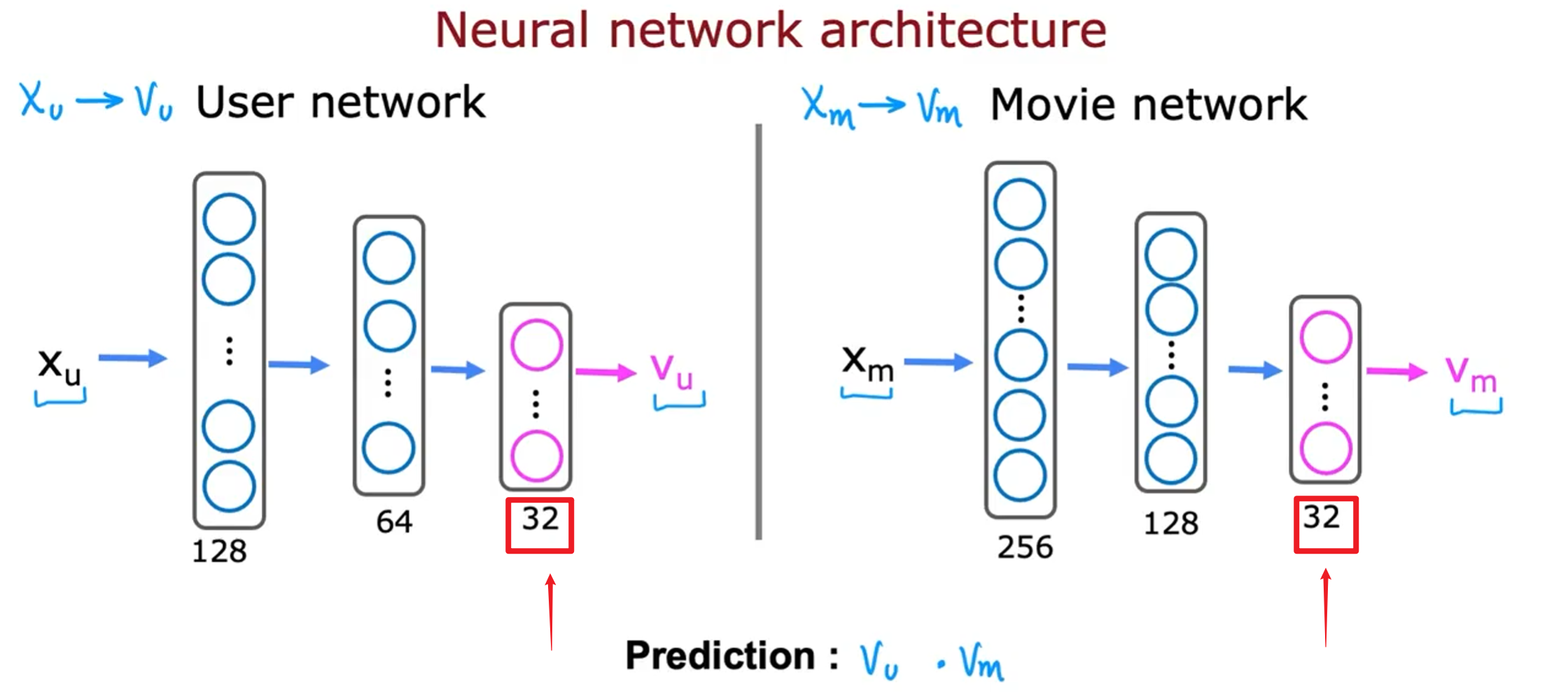
需要注意的是,用户网络和电影网络输出层的神经元个数需要相同,中间的隐藏层可以不同。
$V_u\cdot V_m$ 最终计算出的是1-5或0-5星的电影评级,如果我们有二进制标签,y表示用户喜欢或不喜欢某个项目,可以将sigmod函数应用于$V_u\cdot V_m$ 得出标签为1的概率。$g(v_u\cdot v_m)\mathrm{topredicttheprobabilitythaty^{(i,j)}is1}$
我们也可以将用户网络和电影网络合成一个神经网路,最终直接计算出预测值: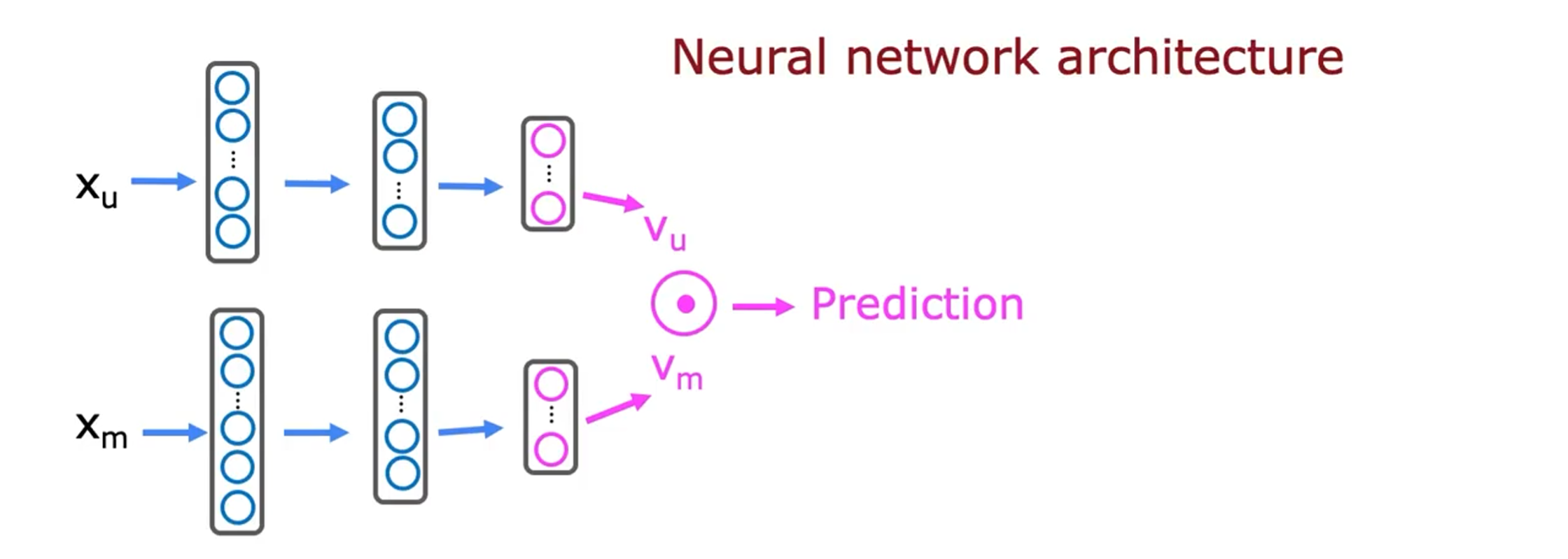
现在,这个模型有很多参数,神经网络的每一层都有一组神经网络参数。那么如何训练用户网络和电影网络的所有参数?我们要做的是构建一个成本函数J。
$$J=\sum_{(i,j):r(i,j)=1}\left(v_{u}^{(j)}\cdot v_{m}^{(i)}-y^{(i,j)}\right)^2+\text{NN regularization term}$$
我们将神经网路算出来的参数 $V_u$ 和 $V_m$ 带入成本函数中的 $v_{u}^{(j)}$ 和$v_{m}^{(i)}$ ,来评价该模型的好坏,进而用梯度下降或其他优化算法来调整神经网络的参数,还可以添加神经网络的正则化项 NN regularization term 来防止过拟合。
当训练完这个神经网络后,也可以用它来寻找相似的电影:

目前该算法的一个局限性是,如果您有大量可能想要推荐的不同电影的大目录,那么运行它的计算成本可能非常高。
从大型目录中推荐
如果要推荐数百万、数千万甚至更多的电影时,如何使算法运行的更高效。 实现为两个步骤,称为检索和排名步骤。
在检索步骤中生成大量可能的项目候选列表,试图涵盖可能向用户推荐的许多可能的东西。如果候选列表中包含很多用户可能不太喜欢的项目,那么在排名步骤中将微调并选择最好的项目推荐给用户。
检索
生成大量可能的候选项目列表
(1)对于用户最近观看的 10 部电影中的每一部电影,查找 10 部最相似的电影
(2)对于观看次数最多的 3 个类型,查找排名前 10 的电影
(3)国内排名前20的电影将检索到的项目合并到列表中,删除重复项和已观看/购买的项目
检索步骤的目标是确保广泛的覆盖范围,以便有足够的电影至少有很多好电影
排名
- 获取检索到的列表,并使用模型进行排名(把用户特征向量和电影特征向量输入到神经网络中)
- 向用户显示排名的项目

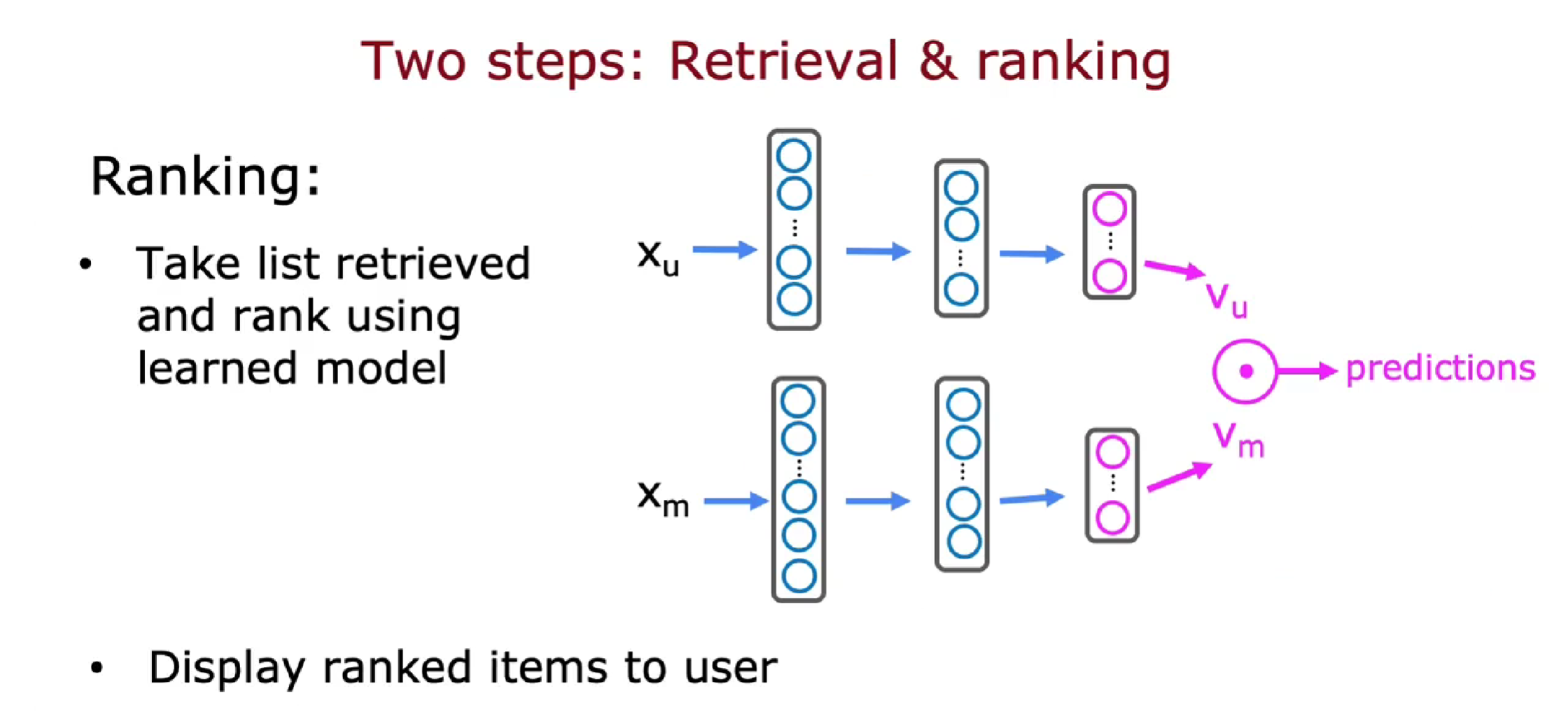
检索更多项目会带来更好的性能,但推荐速度会更慢。
要分析/优化权衡,请进行离线实验,看看检索其他项目是否会产生更相关的推荐。
但是通过单独的检索步骤和排名步骤,能使许多推荐系统能够提供快速和准确的结果。因为检索步骤试图剪掉很多不值得做的更详细的项目,然后排名步骤对用户实际可能喜欢的项目进行更仔细的预测。否则需要对所有的项目进行非常详细的预测。
基于内容过滤的TensorFlow实现
