机器学习05-无监督学习
聚类(Clustering)
聚类算法查看大量数据点并自动找到彼此相关或相似的数据点。
K-means
首先做的是随机初始化集群中心的位置,集群中心称为簇质心(Cluster centroids)。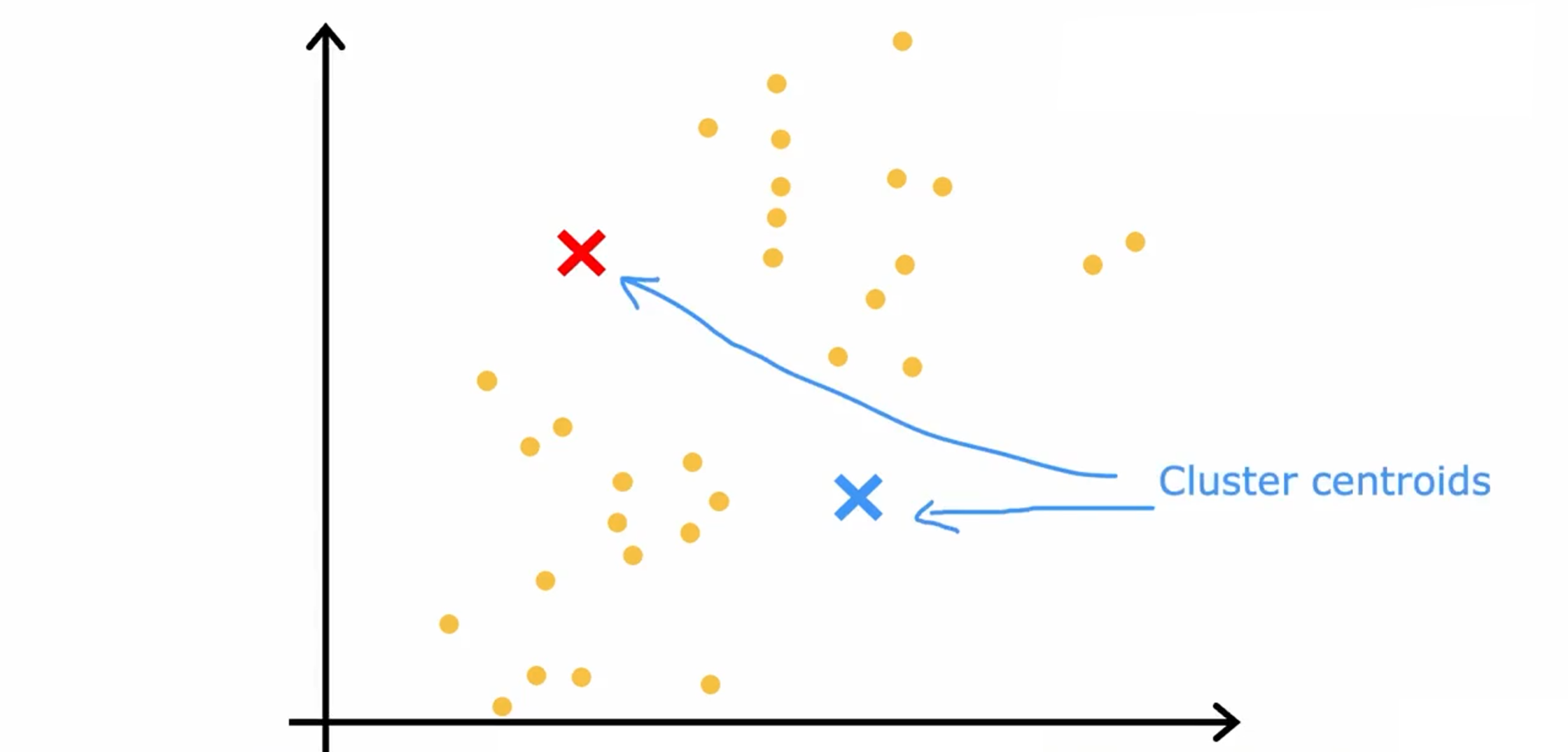
接着,重复做两件事,第一个是将点分配给簇质心,第二个是移动簇质心
第一步:遍历这些点中的每一个,并查看它是更接近红十字还是更接近蓝十字。然后把这些点分配给它更接近的簇质心。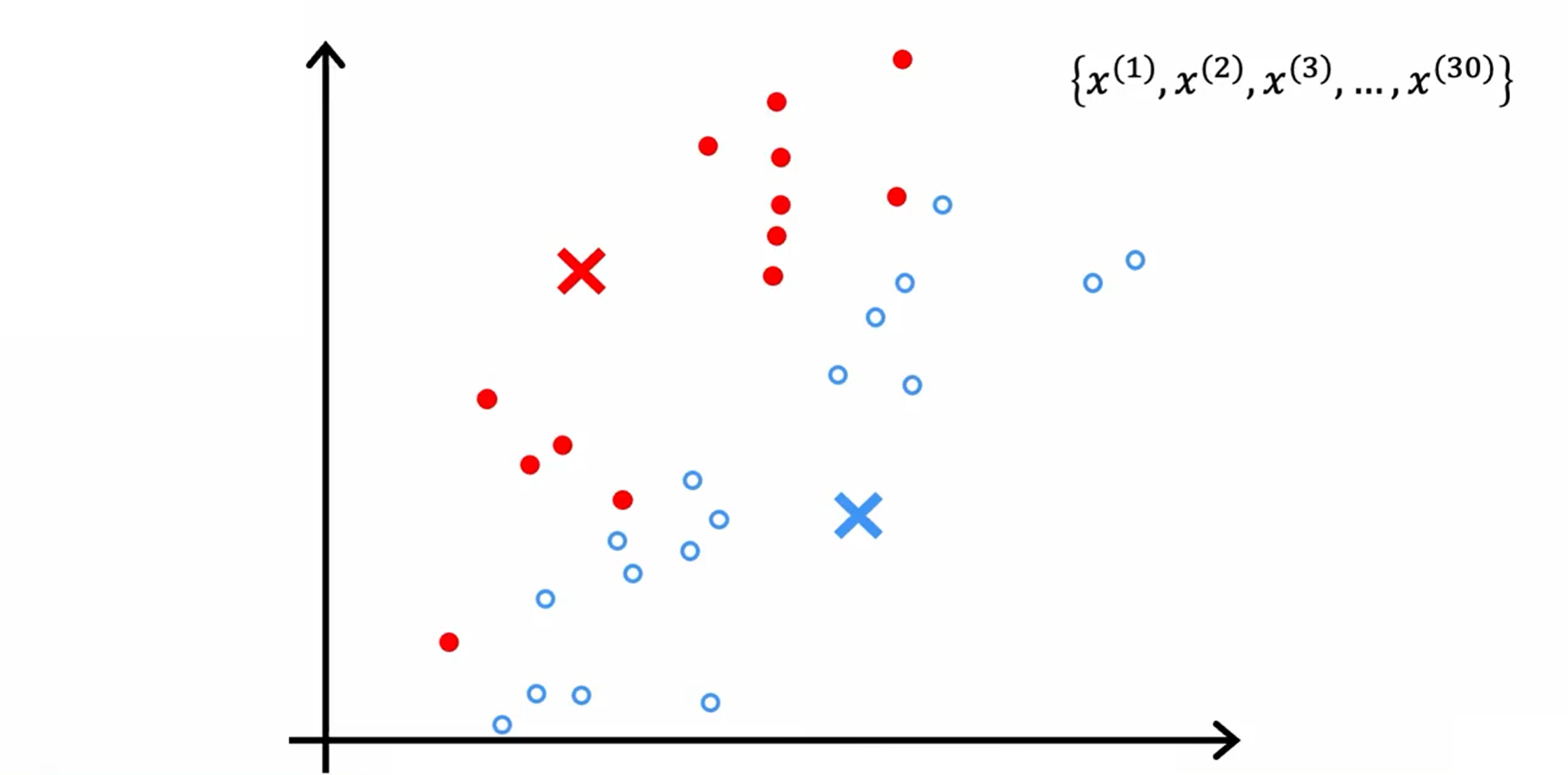
第二步:查看所有的红点并取它们的平均值。并将红十字移动到红点的平均位置,称为新的簇质心位置。蓝色同理。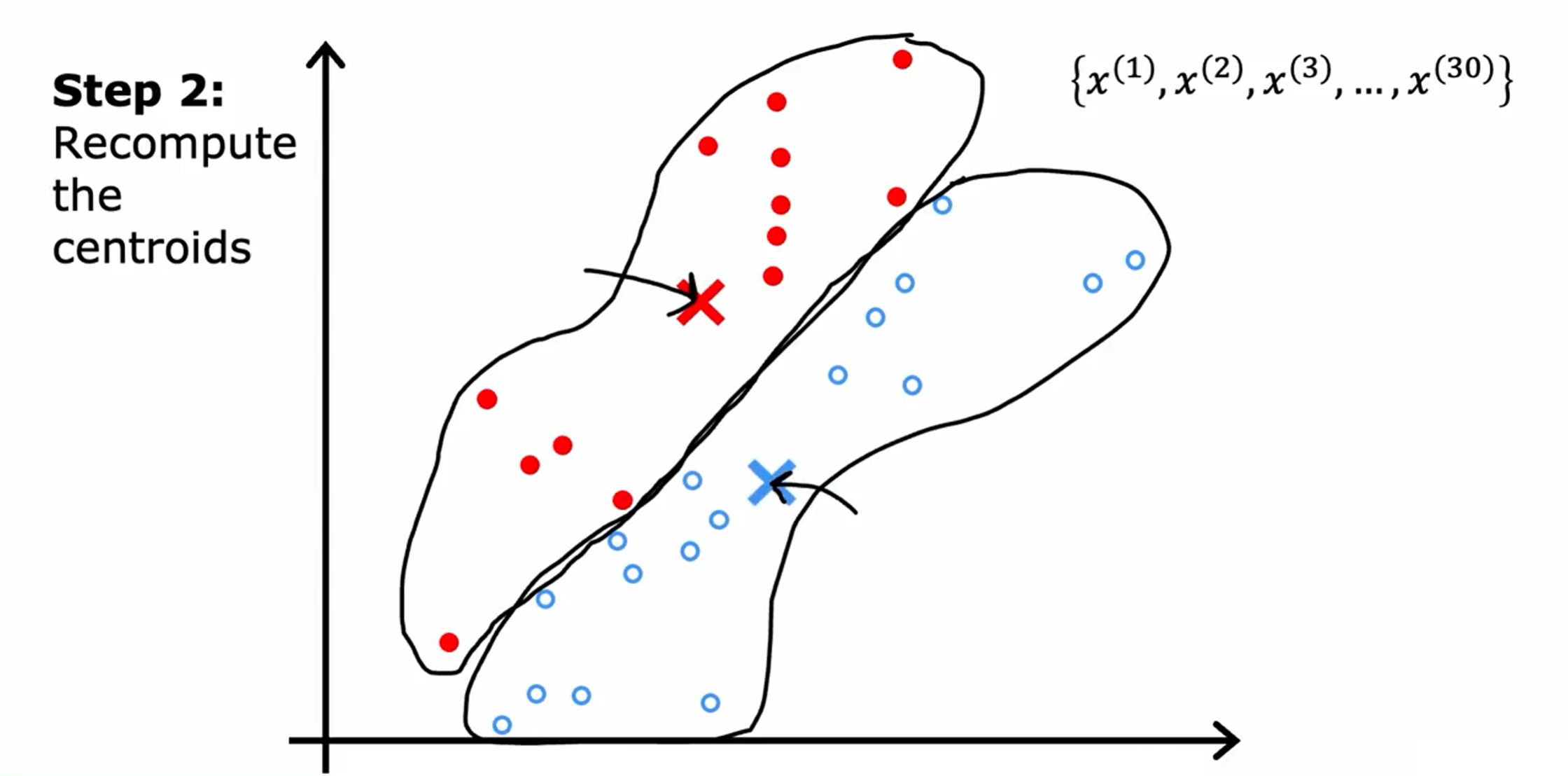
重复第一步:遍历每一个点并分配。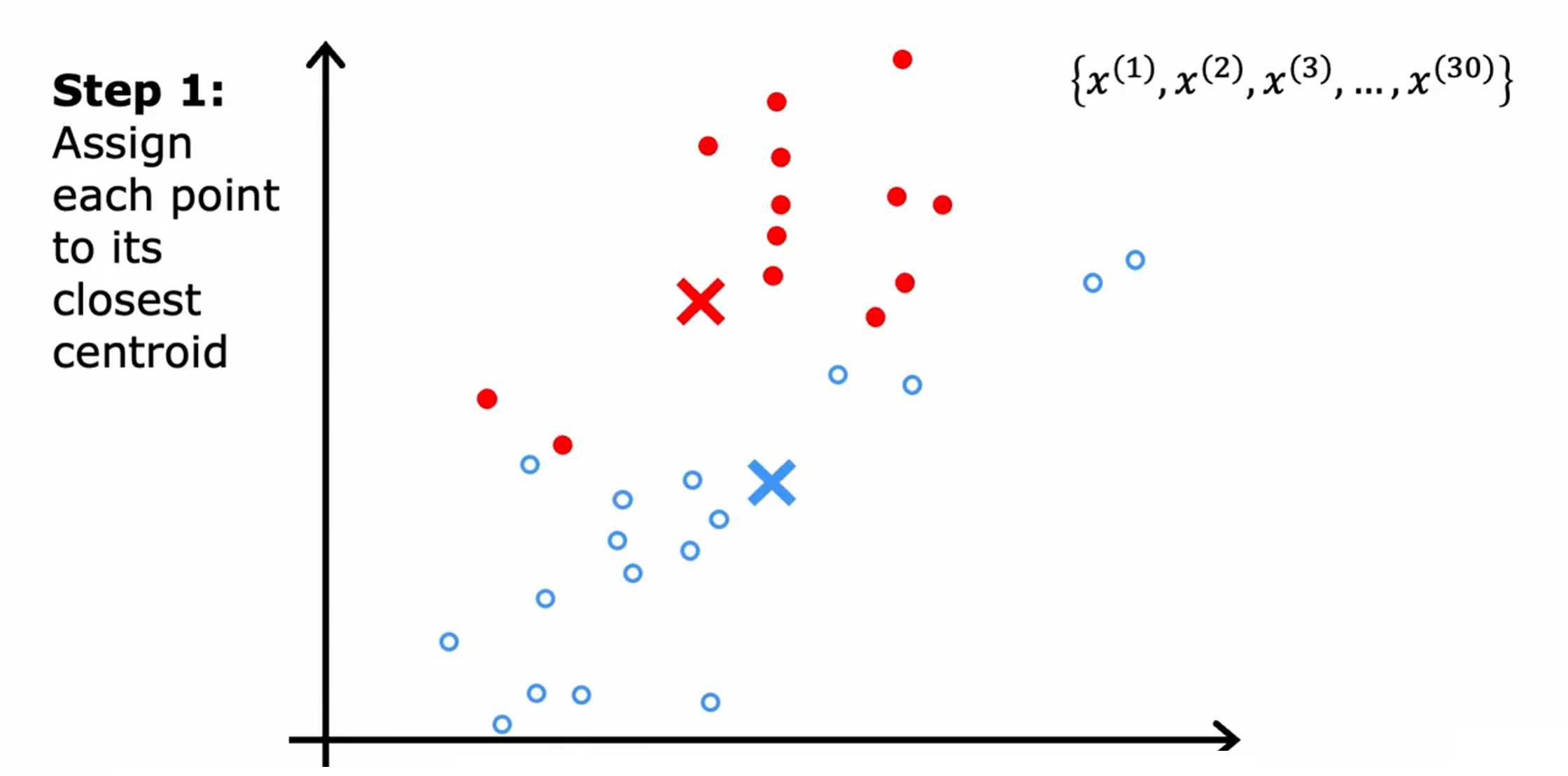
接着重复第二步:移动簇质心。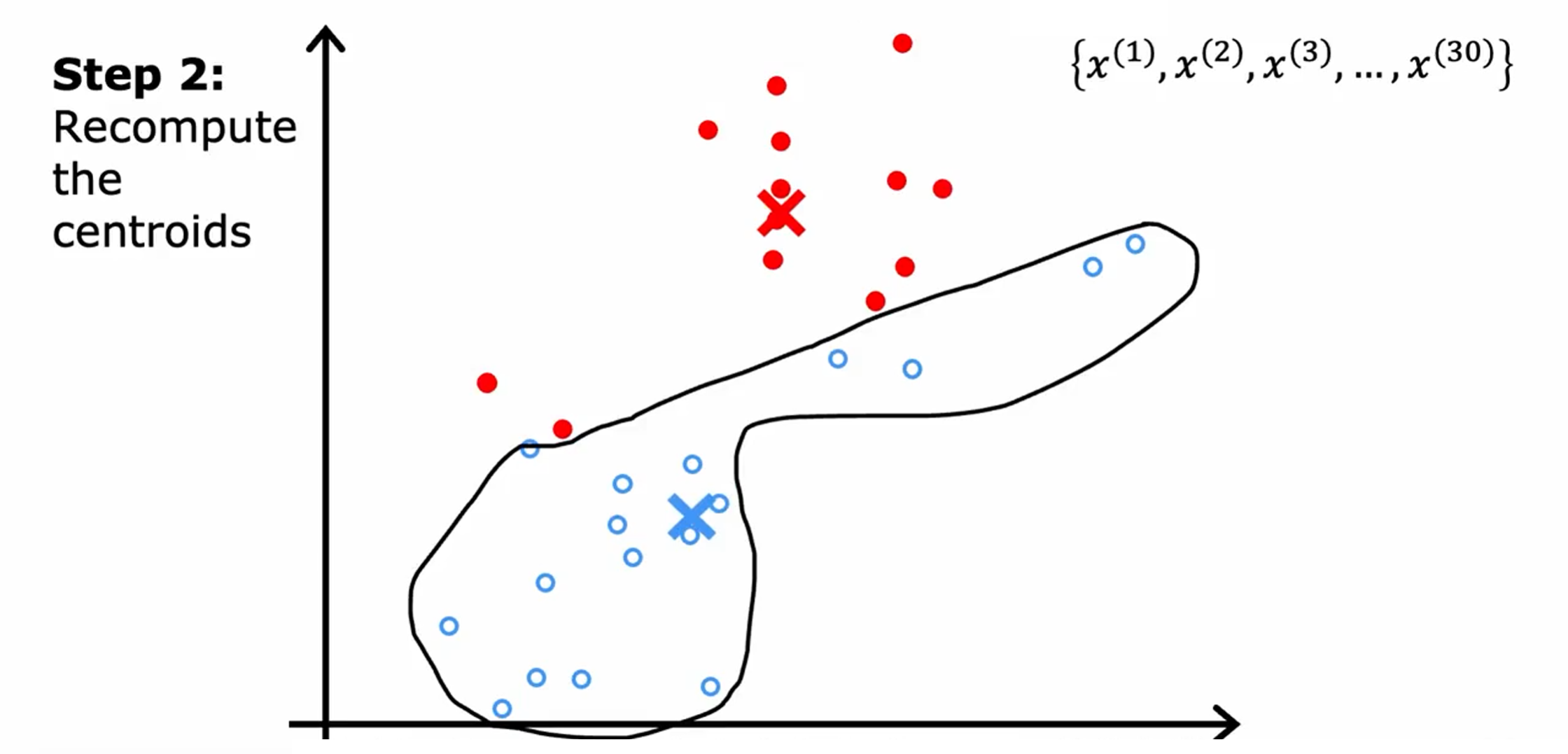
一直重复这两个步骤,直到簇质心的位置没有变化,此时K均值聚类算法已经收敛。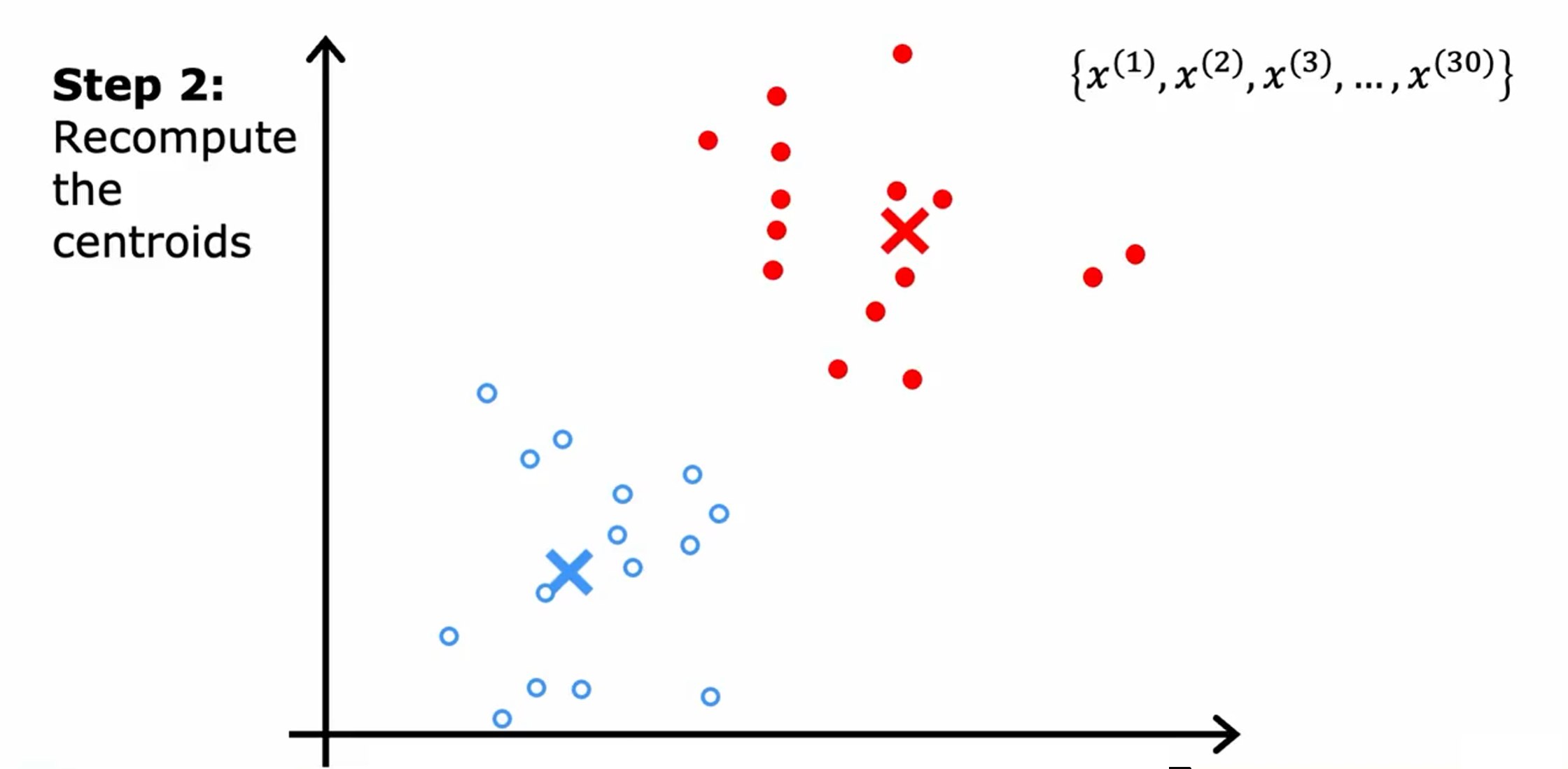
K-means算法
第一步:将点分配给簇质心
K:共K个聚类中心 $\mu_{1},\mu_{2},\ldots,\mu_{K}$
$c^{(i)}$ = 最接近$x^{(i)}$的聚类中心点的索引(从1到K)
例如:点$x^{(1)}$ 离聚类中心 $\mu_{1}$ 最近,则$c^{(i)}$ = 1
第二步:移动簇质心
$\mu_k$ = 分配给群组k的点的平均值
K-means的成本函数
$\mu_{C^{(i)}}$ = 示例$x^{(i)}$所在群组的聚类中心点
$$J\big(c^{(1)},…,c^{(m)},\mu_1,…,\mu_K\big)=\frac{1}{m}\sum_{i=1}^{m}\big\Vert x^{(i)}-\mu_{c^{(i)}}\big\Vert^2$$
m表示训练样本的数量。
$\mu_k$ 和$\mu_{C^{(i)}}$ 区别:
$\mu_k$表示第k个群组的聚类中心点,即将该群组中所有分配给该群组的点$x^{(i)}$的平均值作为新的聚类中心点。$\mu_k$的计算方式是通过对属于第k个群组的所有数据点的均值来获得。
而$\mu_{C^{(i)}}$表示示例$x^{(i)}$所在群组的聚类中心点,是通过将$x^{(i)}$分配给最近的聚类中心点得到的。$\mu_{C^{(i)}}$和$\mu_k$具有相同的含义,只是对应于不同的数据点。$\mu_{C^{(i)}}$是根据每个数据点$x^{(i)}$的分配结果得到的,而$\mu_k$是根据整个群组的数据点求取均值得到的。
因此,$\mu_{C^{(i)}}$和$\mu_k$在K-means算法中都用于表示聚类中心点,只是对应于不同的数据点和群组。$\mu_{C^{(i)}}$表示一个特定的数据点的聚类中心点,而$\mu_k$表示整个群组的聚类中心点。
如何初始化簇质心
随机选择样本点作为初始簇质心
只选择一次的话容易陷入局部最优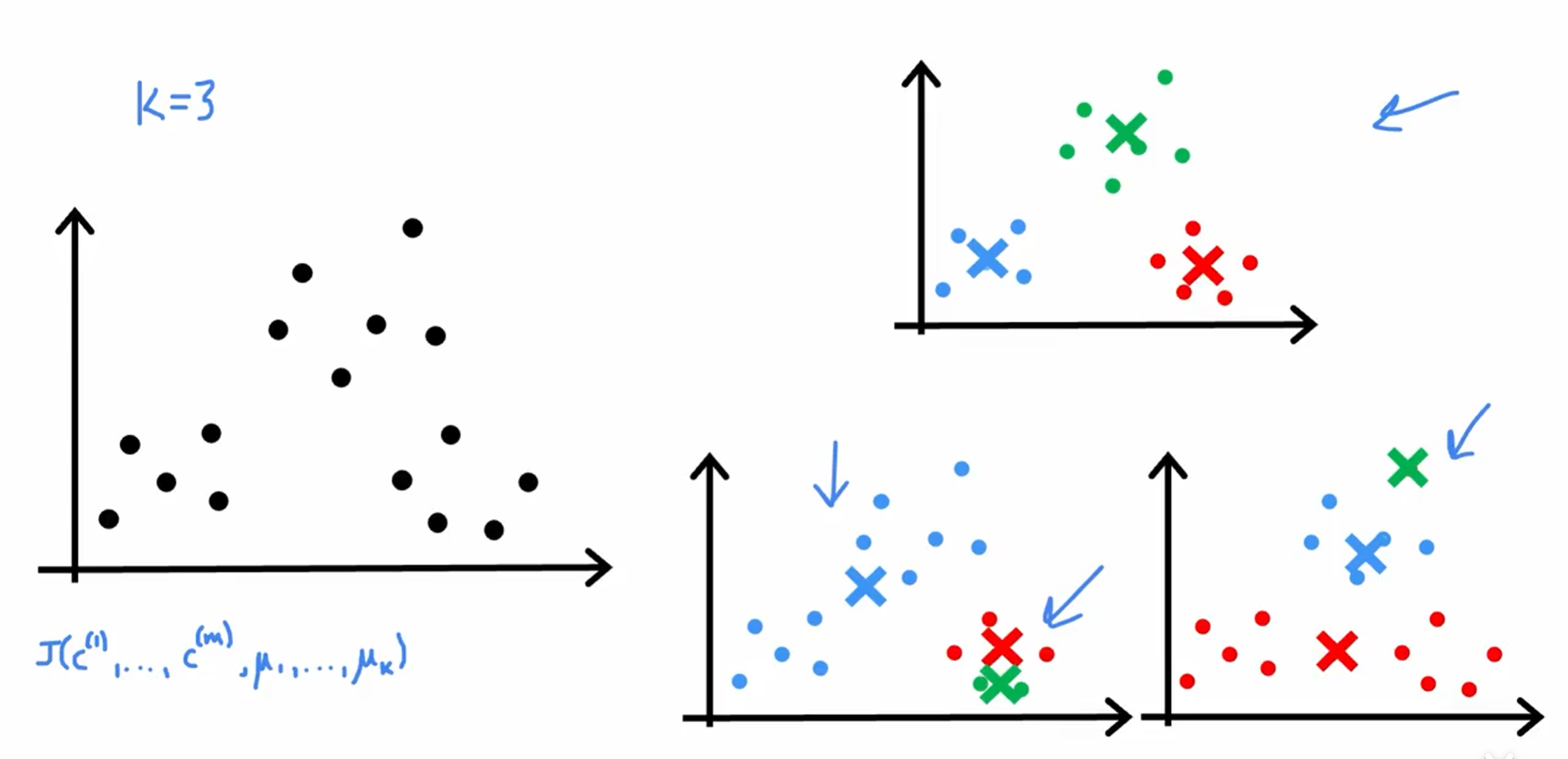
多次选择样本点作
为簇质心,最终选择出成本函数最小的那一个
选择聚类数量K
Elbow method: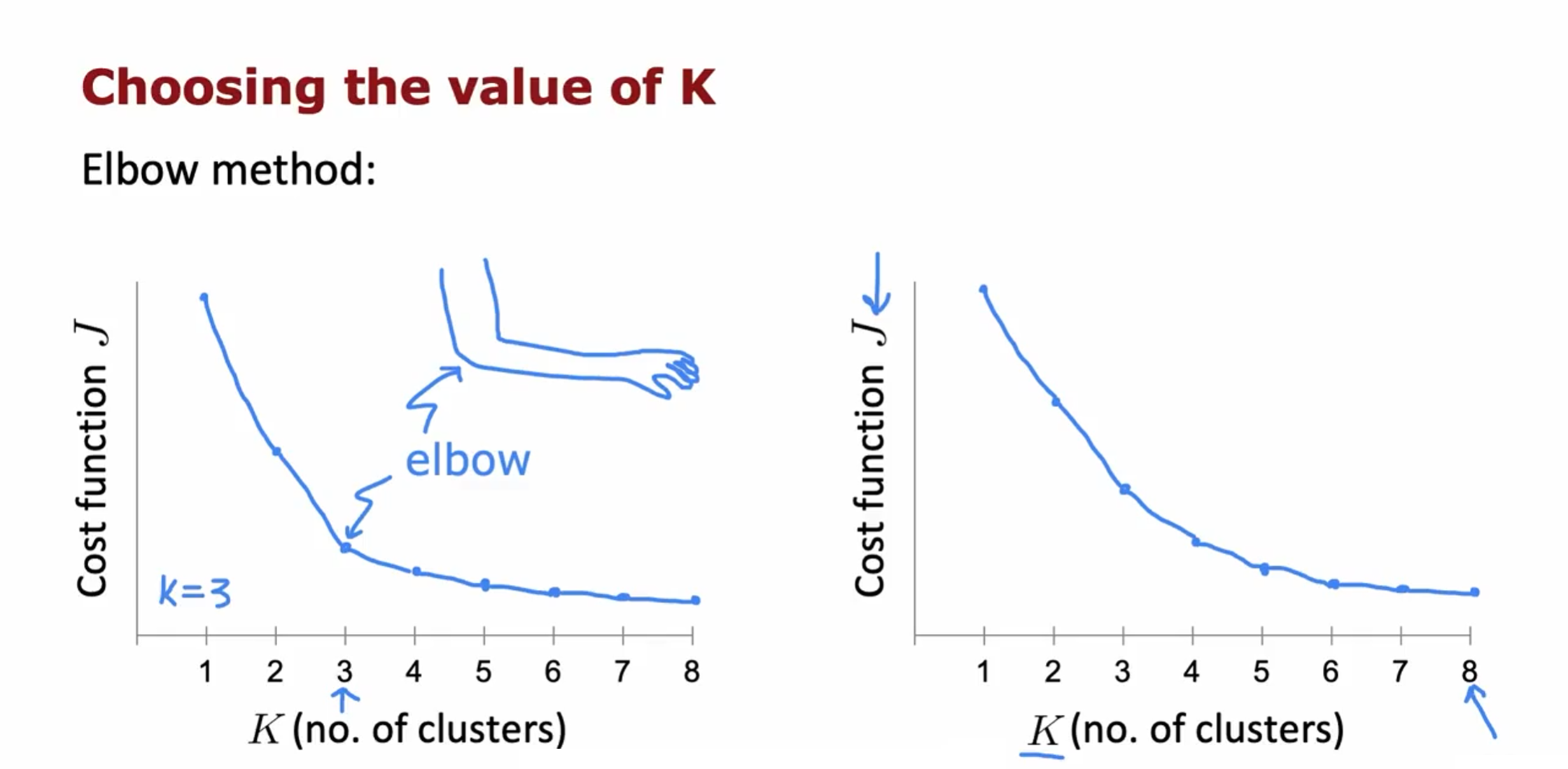
对于将T恤分成三个尺码,还是五个尺码,需要考虑成本和利润之间的关系,五个尺码可能挣得更多,但是成本更大。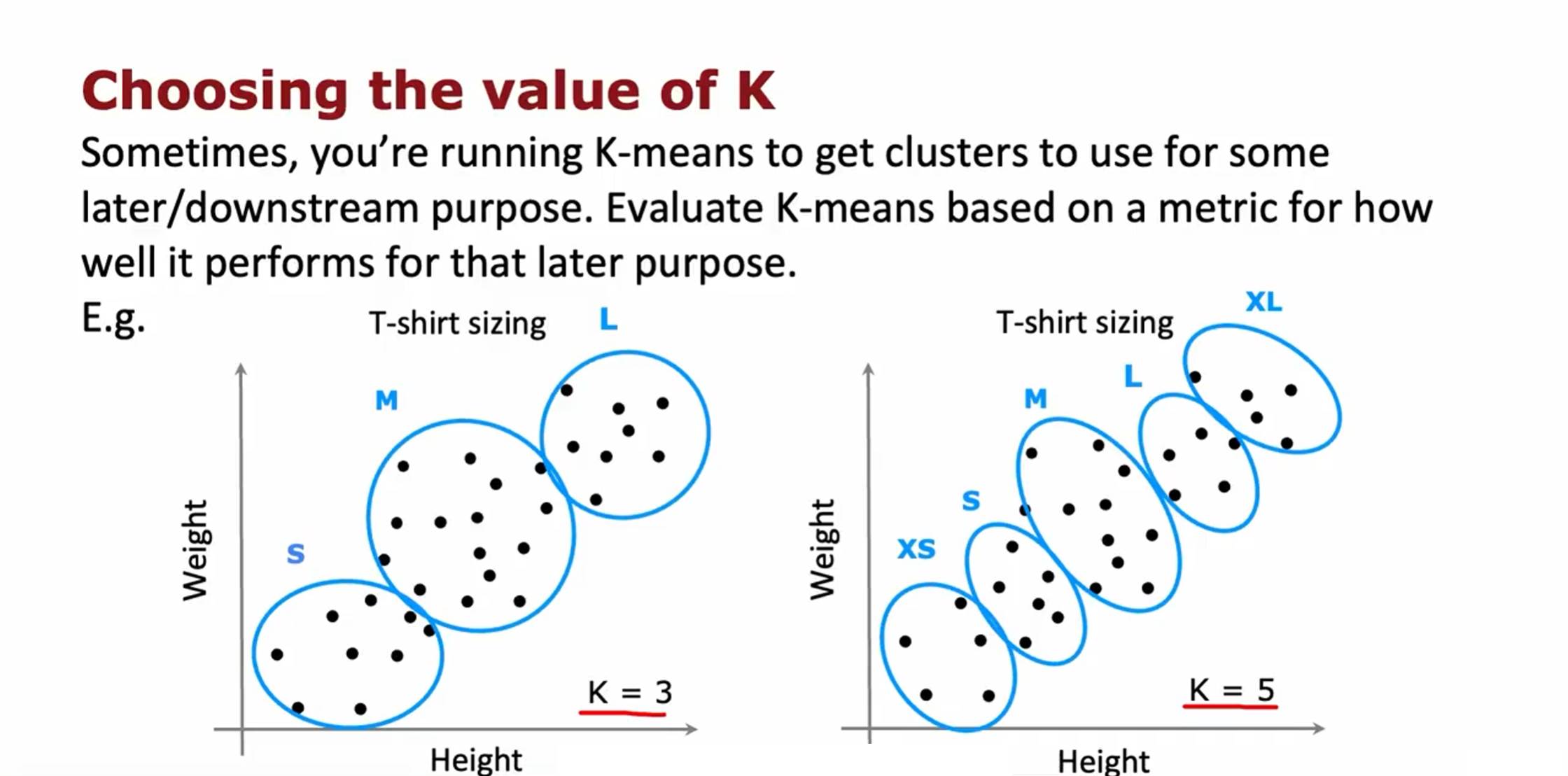
异常检测(Anomaly detection)
异常检测(Anomaly Detection)是一种用于识别和监测数据中异常、异常行为或异常模式的技术。它可以帮助我们在大量数据中自动发现那些与正常行为或模式不同的数据点。
检测制造的飞机发动机是否存在问题,为了简化问题,我们以发动机运行的温度、震动频率作为特征。当新引擎的参数落在中间一堆时,发动机正常,当落在外围时有很大概率存在问题。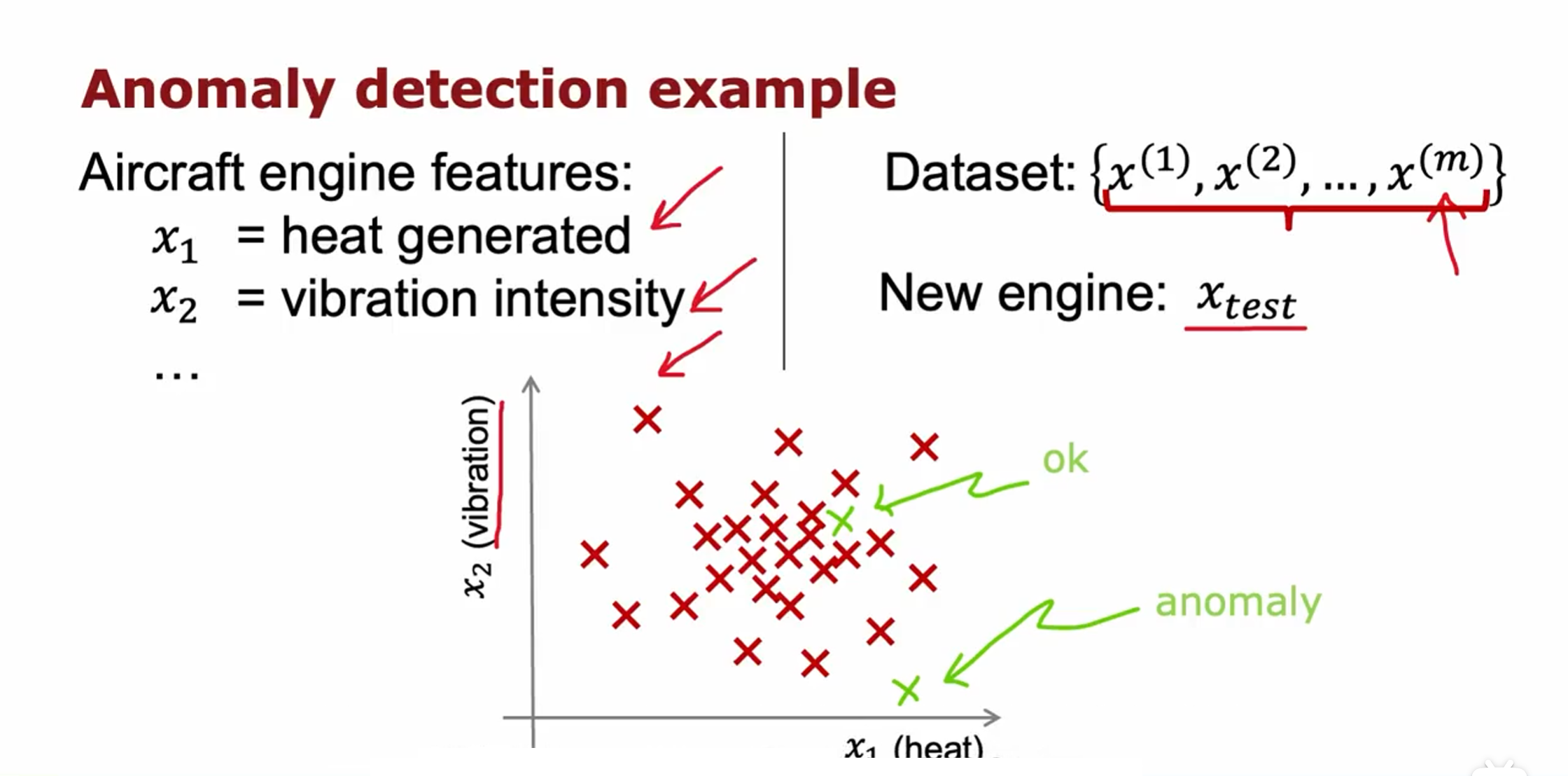
执行异常检测的最常见方法是通过密度估计的技术。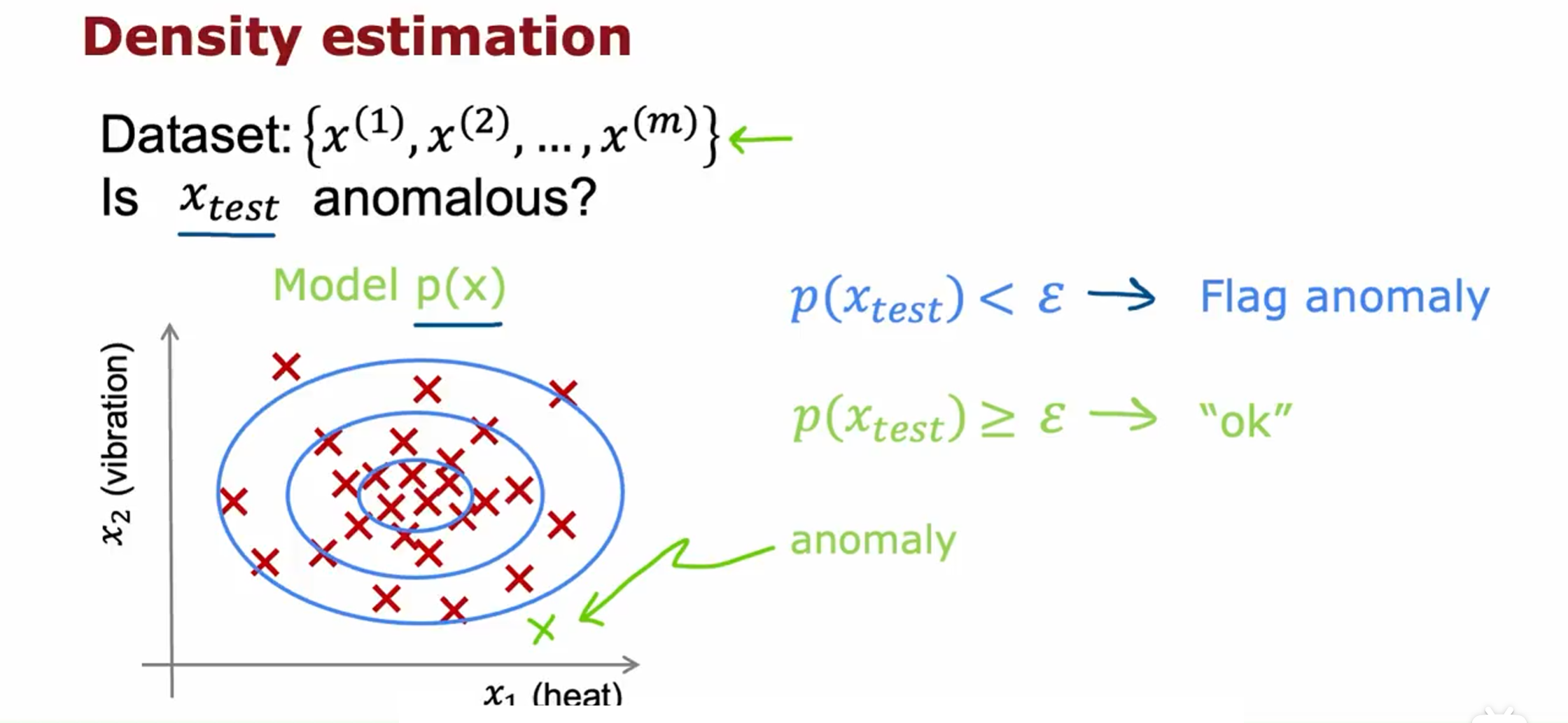
高斯分布
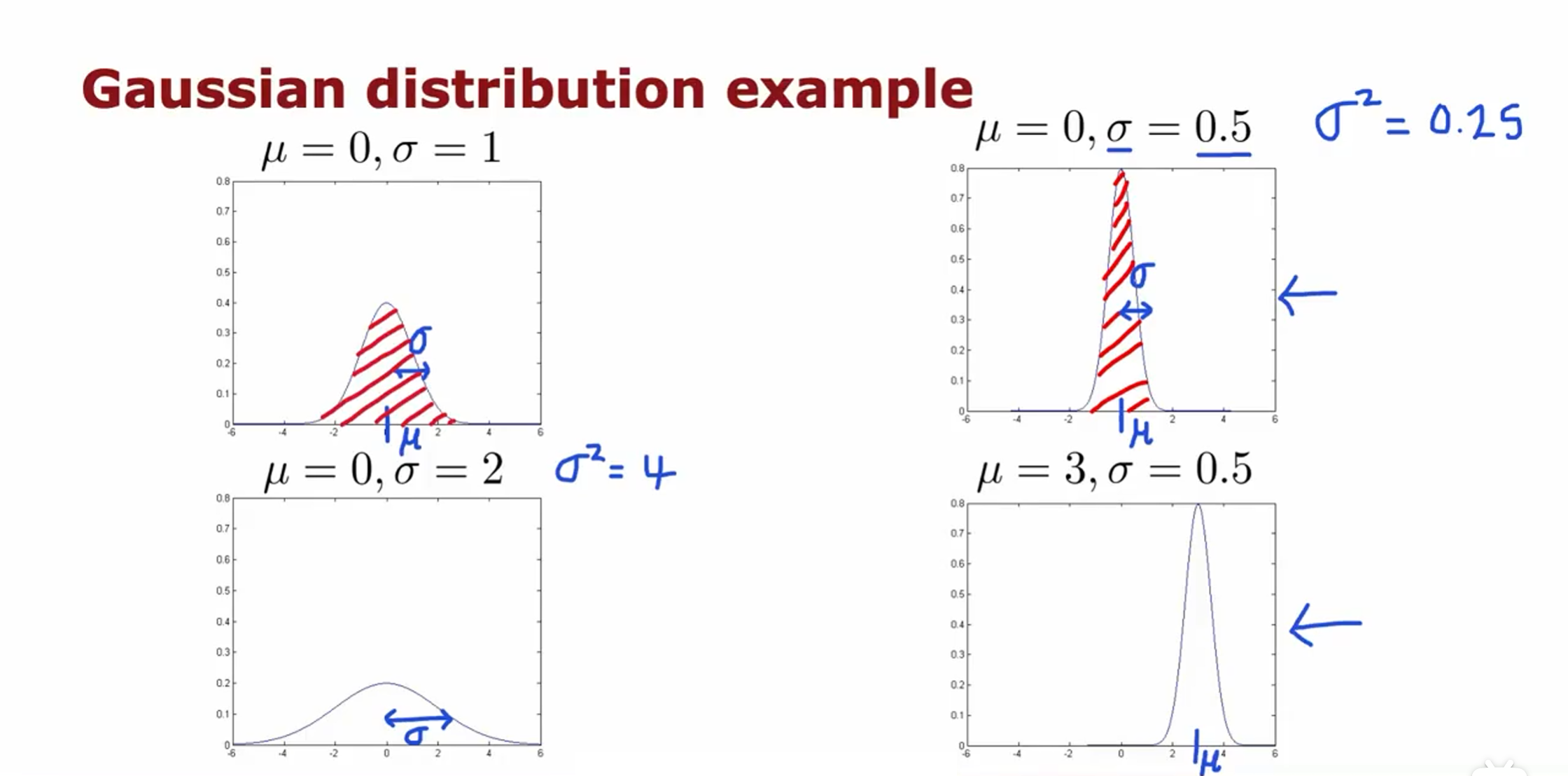
对于只有一个特征时,将其应用于异常检测,就是要找到参数 $\mu$ 和 $\sigma^2$ 的合适取值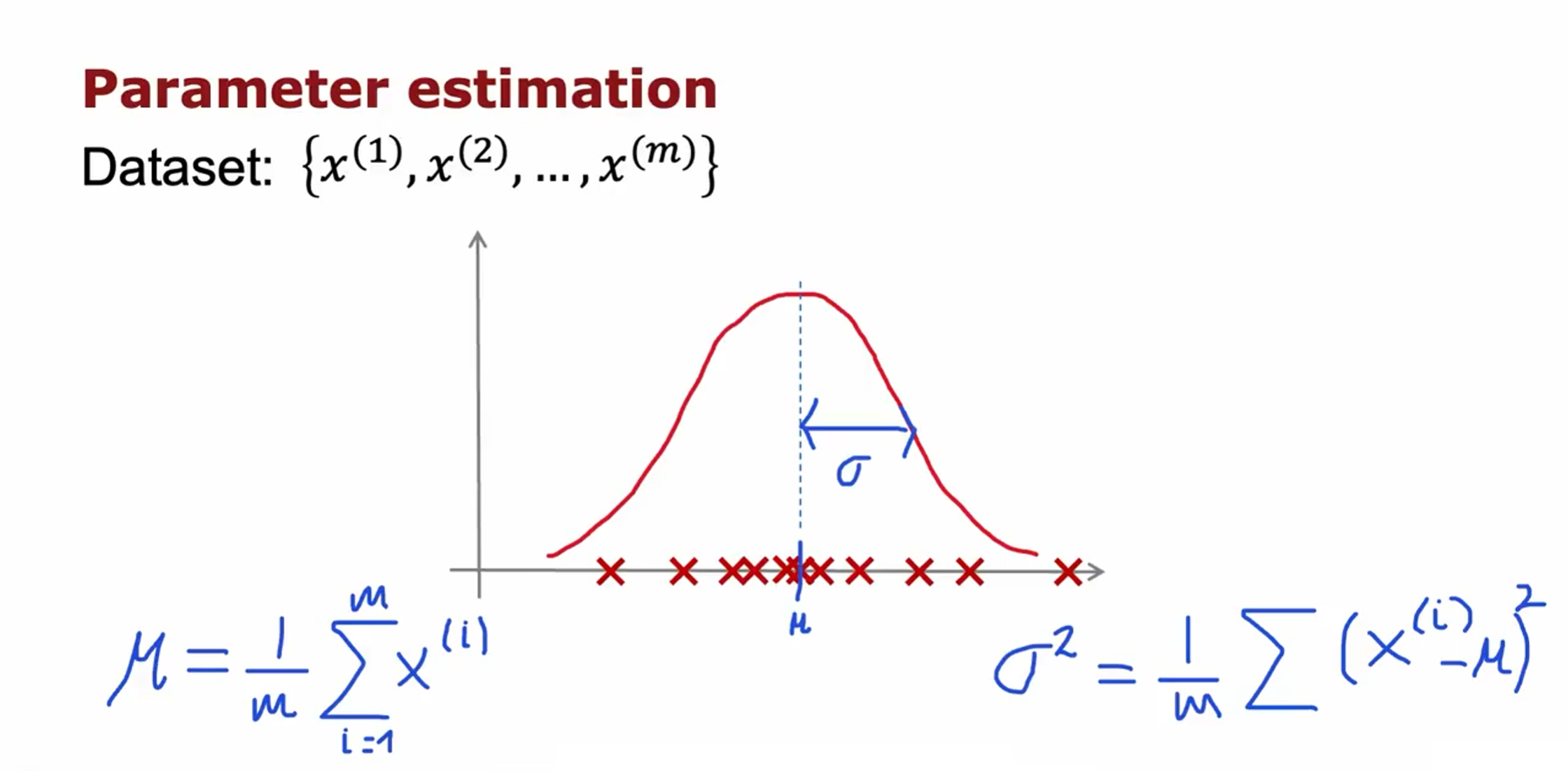
异常检测算法

共有m个样本,n个特征,对每一个特征求平均值 $\mu$ 和方差 $\sigma^2$ 。
$\mu_j$ : 第j个特征的平均值
$\sigma_j^2$ : 第j个特征的方差
$p(x)$ : 假定每一个特征 $x_{1}$ 到 $x_{n}$ 均服从正态分布,则其模型的概率为:
$$\begin{aligned}
p(x)& =p(x_{1};\mu_{1},\sigma_{1}^{2})p(x_{2};\mu_{2},\sigma_{2}^{2})\cdotp\cdotp\cdotp p(x_{n};\mu_{n},\sigma_{n}^{2}) \
&=\prod_{j=1}^{n}p(x_{j};\mu_{j},\sigma_{j}^{2}) \
&=\prod_{j=1}^{n}\frac{1}{\sqrt{2\pi}\sigma_{j}}exp(-\frac{(x_{j}-\mu_{j})^{2}}{2\sigma_{j}^{2}})
\end{aligned}$$
举例:
假定我们有两个特征,它们都服从于高斯分布,并且通过参数估计,我们知道了分布参数: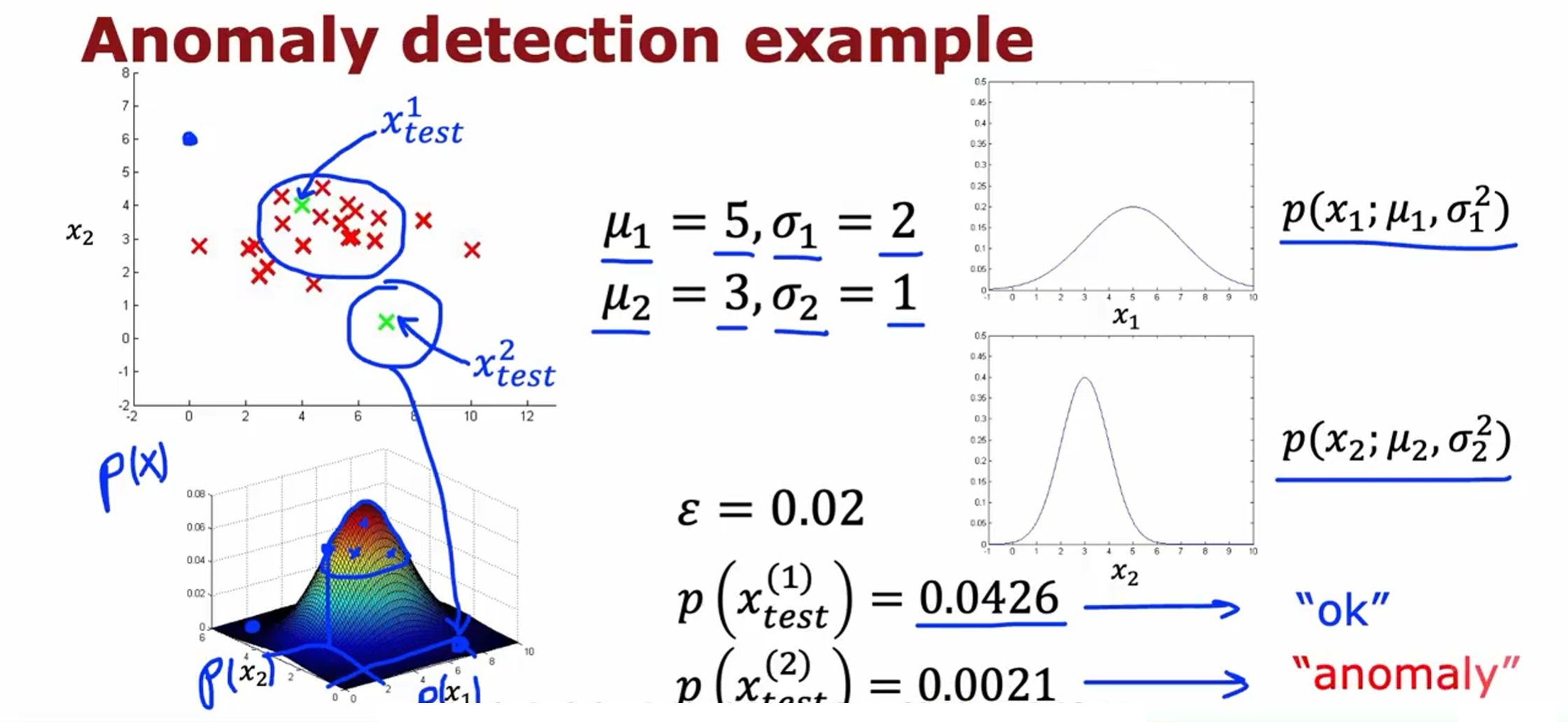
将 $p(x_1;\mu_1,\sigma_1^2)$ 和 $p(x_2;\mu_2,\sigma_2^2)$ 相乘后会得到上图左下角的三维曲面图 $p(x)$。当 $p\left(x_{test}^{(1)}\right)$ 小于 $\mathbf{\varepsilon}$ 时,有异常。
算法评估
实数计算

飞机发动机监测实例:
根据以往的数据,我们选择10000个正常的样本,20个异常样本。
在训练集中用6000个正常样本训练模型;
交叉验证集中有2000个正常数据和10个异常数据,并把它们标记为0和1。在交叉验证集中评估模型准确率。
接着,改变超参数,训练集中训练模型,交叉验证集中评估模型。
最后选出一个最好的模型用在预测集中评估最终模型。
算法评估
如果负面样本非常少,也可以不用预测集,只用训练集和交叉验证集。但这样的弊端是,模型可能在未知的数据上效果并不好。
由于异常样本是非常少的,所以整个数据集是非常偏斜的,我们不能单纯的用预测准确率来评估算法优劣,所以用我们之前的查准率(Precision)和召回率(Recall)计算出 F 值进行衡量异常检测算法了。
- 真阳性、假阳性、真阴性、假阴性
- 查准率(Precision)与 召回率(Recall)
- F1 Score
异常检测VS监督学习

异常检测,任何偏离正常的情况都被标记为异常,包括这在您的数据集中从未见过的一种全新的飞机发动机故障方式。
无监督适用于可能会出现从来没见过的例子的事情,而监督学习就适用于不会出现和以前完全不一样的例子的数据集
异常检测试图找到全新的正面示例,这些示例可能与您以前见过的任何东西都不一样。监督学习会查看您的正面示例并尝试确定未来示例是否与您已经看到的正面示例相似,
例子
选择特征
- 将不符合高斯分布的特征转换成符合高斯分布的特征
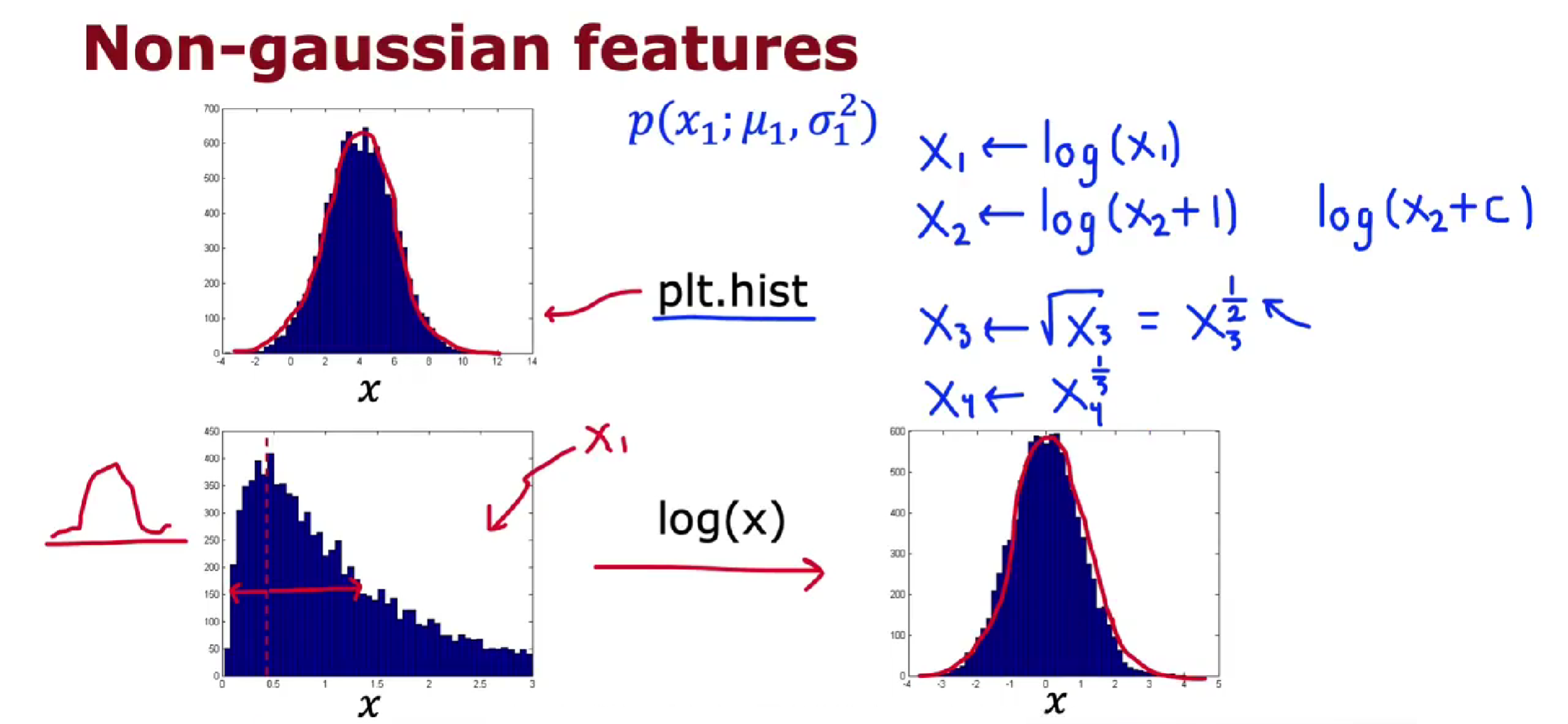
- 查看未能检测出来的异常,然后看看能否寻找出新的特征

PCA算法
降低特征数量
PCA是一种降维算法,用于获取具有大量特征、大量维度或高维度的数据,并将其简化为两个或三个特征,变成二维或三维数据,以便可以对其进行绘图和可视化,并更好地理解数据中有什么。
示例
如果你有来自汽车的数据,并且汽车可以有很多特征。例如汽车的长度,汽车的宽度,汽车的高度,车轮的直径,以及其他特征。如果想要减少特征的数量以便将其可视化,如何使用PCA来做到这一点?
示例1:
假设您有一个具有两个特征的数据集。特征 $x_1$ 是汽车的长度,特征$x_2$ 是汽车的宽度。
在大多数国家/地区,由于对汽车行驶道路宽度的限制,汽车宽度往往变化不大。你会发现数据集 $x_1$ 变化很大,而 $x_2$ 变化相对较小。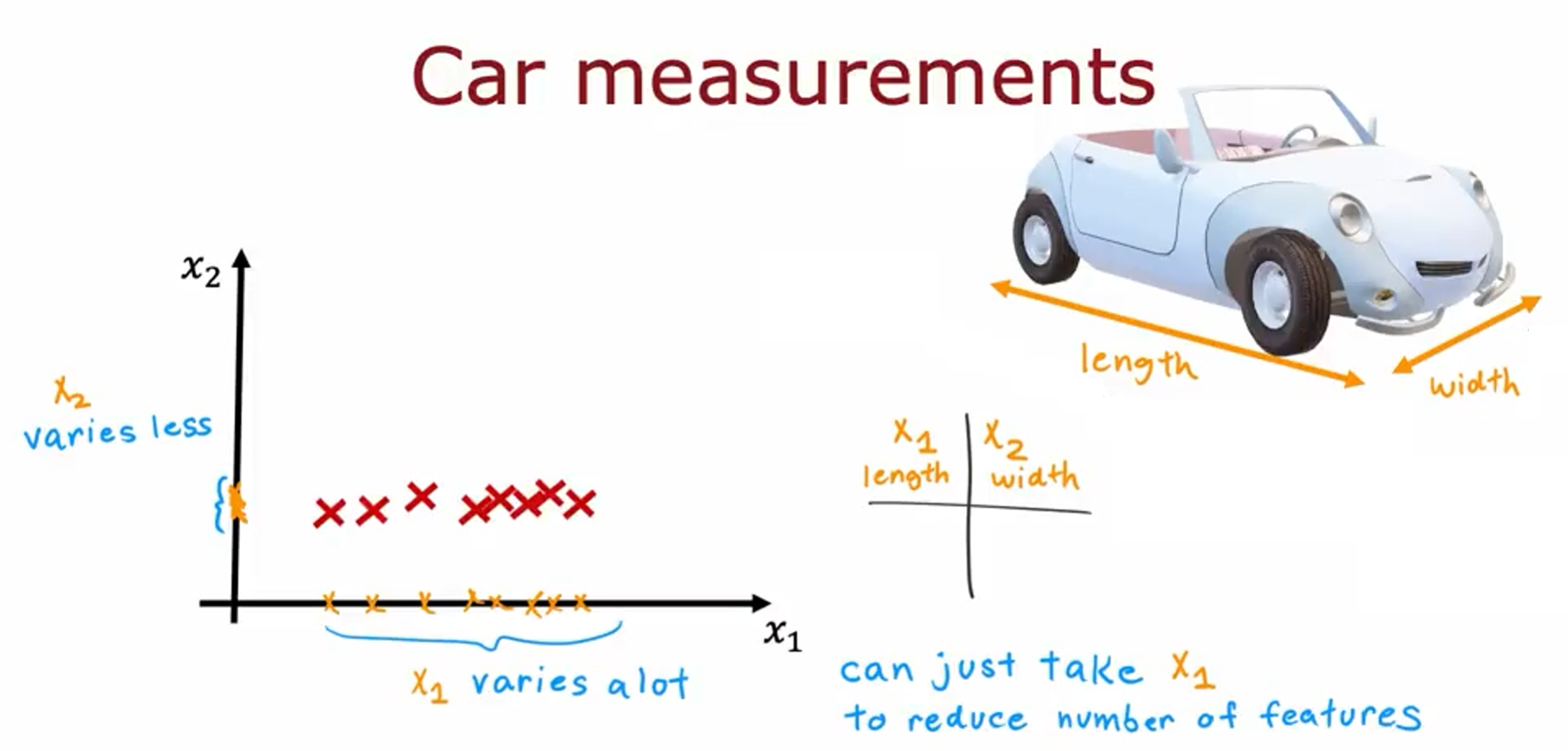
如果你想减少特征的数量,那么,你可以做的一件事就是只取 $x_1$ ,忽略 $x_2$ 。
示例2:
假设我们有两个特征,即汽车的长度 $x_1$ 和高度 $x_2$。这两个特征的变化范围都比较大。如果我们绘制这些数据点,可能会得到一个这样散点图。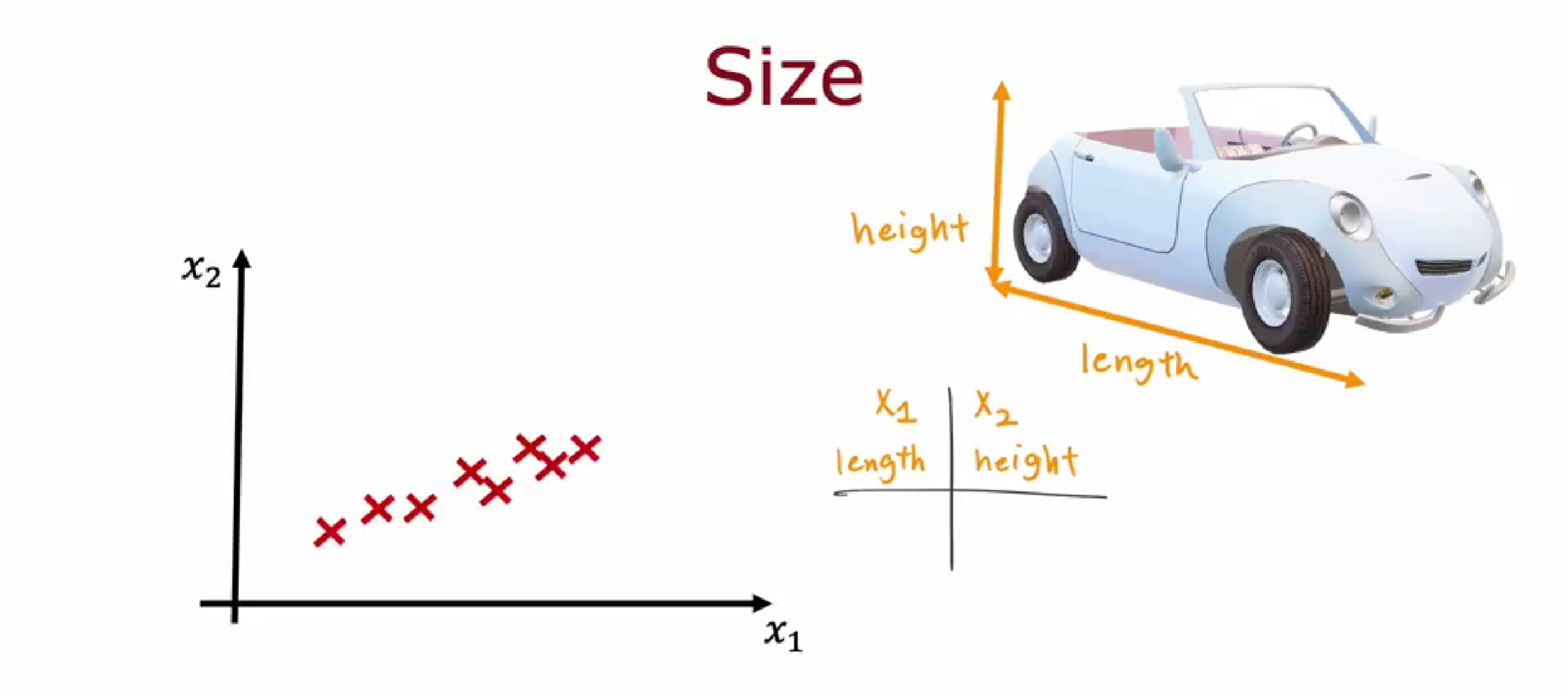
现在,如果我们想要减少特征的数量,我们应该选择什么呢?
我们不希望只选择长度 $x_1$ 而忽略高度 $x_2$,也不希望只选择高度 $x_2$ 而忽略长度 $x_1$。为了解决这个问题,PCA算法提出了一个思想:寻找一个新的轴,我们可以将其称为Z轴。请注意,这里的Z轴并不是在三维空间中突出显示的Z轴,而是长度和高度的组合,也是在这个二维平面中的。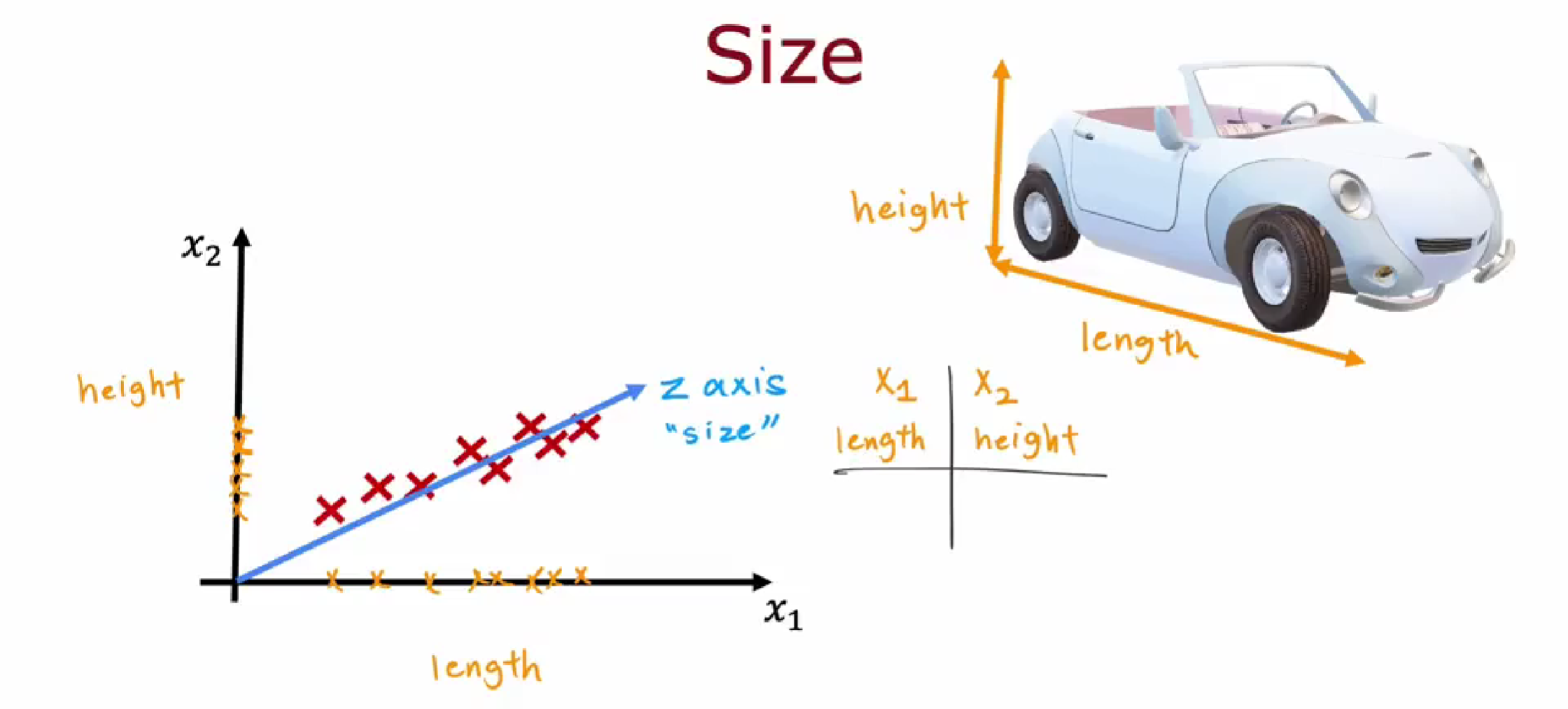
Z轴能够获得关于长度和高度的信息。Z轴上的值可以映射到 $x_1$ 轴和 $x_2$ 轴, $x_1$ 轴上的这个距离是多少,可以告诉我们汽车的长度是多少;$x_2$ 轴上的这个距离是多少,告诉我们汽车的高度是多少。
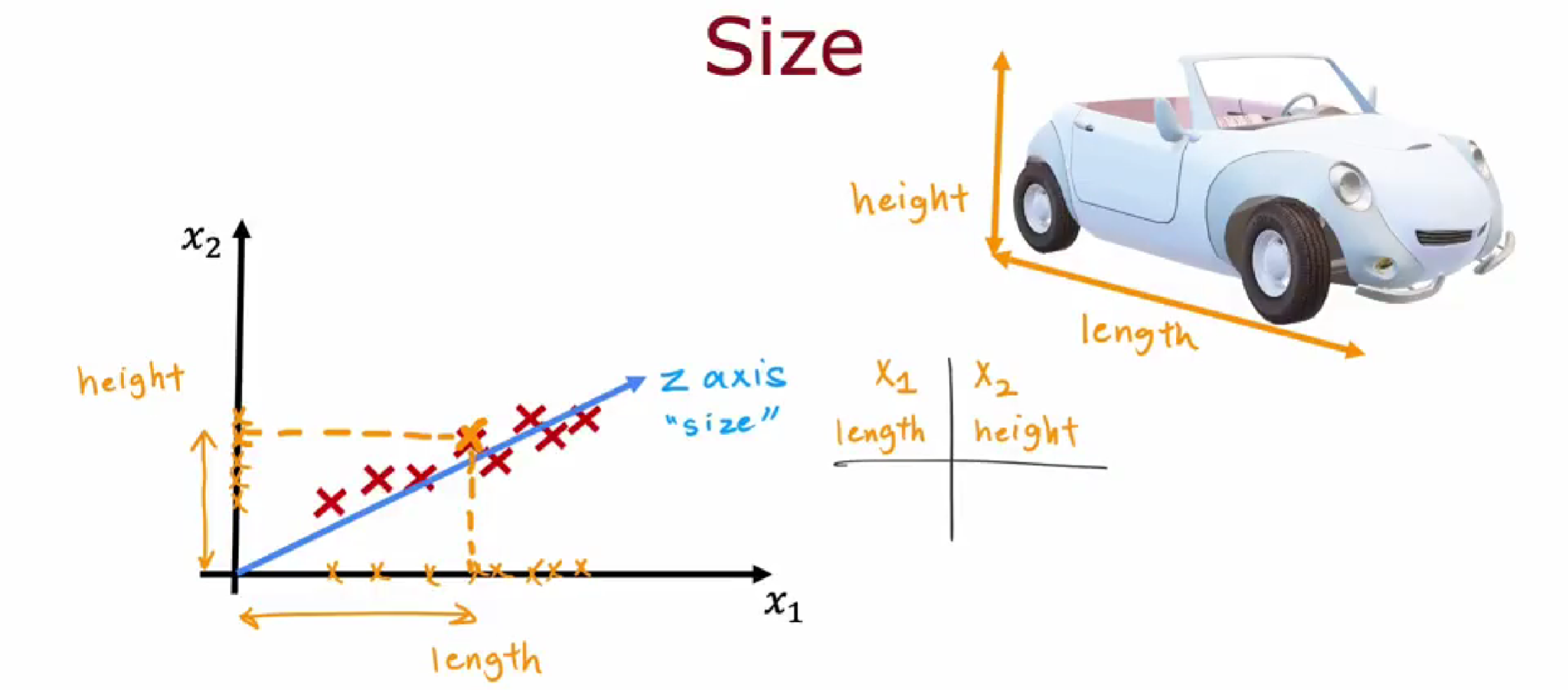
现在,我们只需要一个数字即可反映出汽车的长度和高度的特征。
重建可以知道原来的特征数据(近似的)是多少。这些新轴即为主成分。
通过PCA算法,我们能够将原始高维数据映射到低维空间,将数据的维度减少到我们所选择的新轴上,同时保留了关键的信息。这样做有助于简化问题、减少计算复杂性,并且仍然能够提供有关汽车尺寸的重要特征。
PCA代码实现(scikit-learn)
2D to 1D
2D to 2D
线性回归和PCA区别
线性回归是求绿色线最小值
PCA求黄色线最小值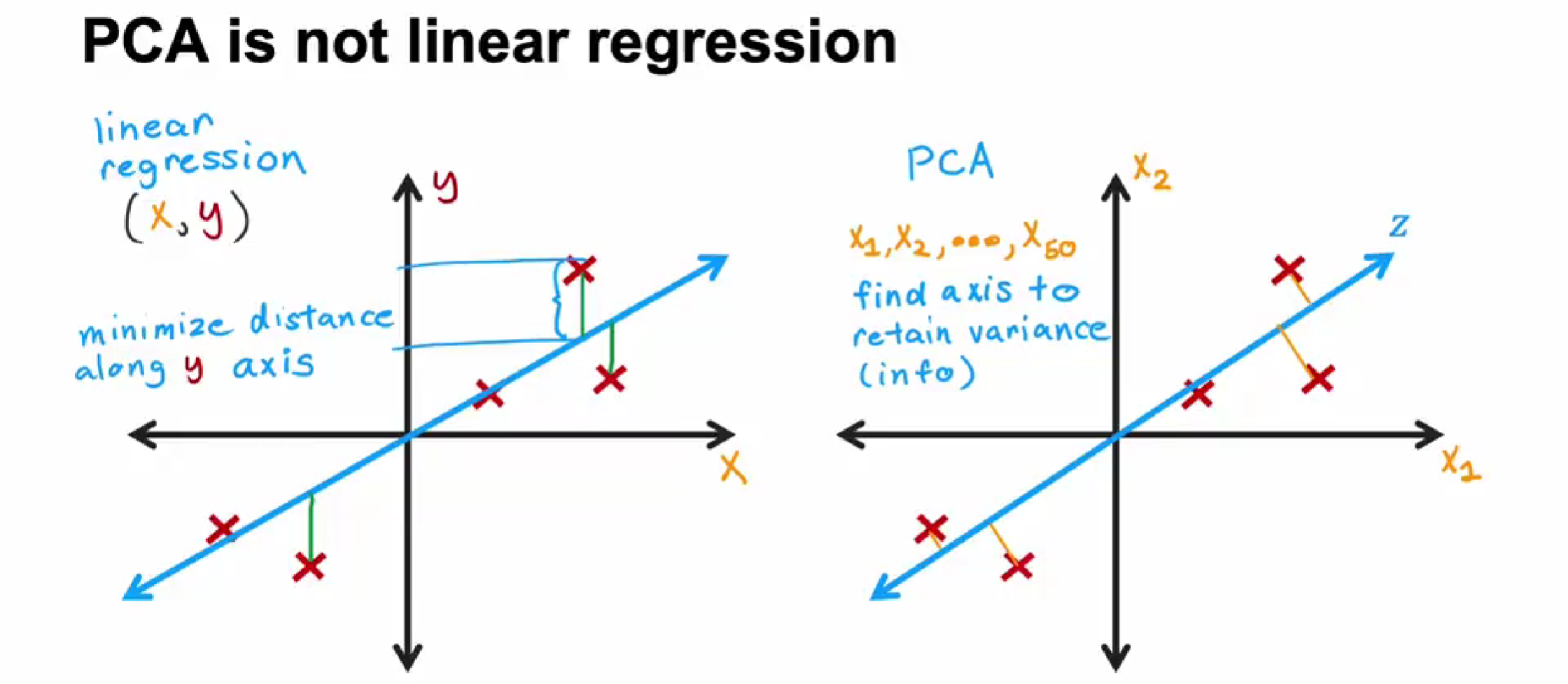
应用PCA的建议
